
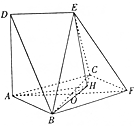
 如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF,且∠DAF=90°.
如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF,且∠DAF=90°.分析 (1)连结EO,推导出四连形DEOA是平行四边形,从而DA∥EO,推导出EO⊥平面ABFC,从而EO⊥AF,由正方形性质得AF⊥BC,从而AF⊥平面BCE,由此能证明DE⊥平面BCE.
(2)取BF的中点G,连结OG,则OG⊥BF,连结EG,过O作OM⊥EG于M,三棱锥A-BCH的体积VA-BCH=VH-ABC,由此能求出结果.
解答 证明:(1)连结EO,∵AF=2$\sqrt{2}$,DE=$\sqrt{2}$,
∴DE$\underset{∥}{=}$AD,∴四连形DEOA是平行四边形,∴DA∥EO,
∵平面DAFE⊥平面ABFC,且平面DAFE∩平面ABFC=AF,
∠DAF=90°,∴DA⊥平面ABFC,∴EO⊥平面ABFC,
∵AF?平面ABFC,∴EO⊥AF,
在正方形ABFC中,∵AF⊥BC,EO∩BC=O,∴AF⊥平面BCE,
∵DE∥AF,∴DE⊥平面BCE.
解:(2)取BF的中点G,连结OG,则OG⊥BF,连结EG,过O作OM⊥EG于M,
∵EO⊥平面BOF,∴EO⊥BF,∴BF⊥平面EOG,
∴BF⊥OM,∴OM⊥平面BEF,∴H与M重合,
在Rt△EOG中,EO=2,OG=1,EG=$\sqrt{5}$,
由OG2=HG×EG,得HG=$\frac{\sqrt{5}}{5}$,∴HG=$\frac{1}{5}EG$,
过H作HK⊥OG,垂足为K,则HK⊥平面ABF,交OG于K,则HK∥EO,
且HK=$\frac{1}{5}EO$=$\frac{2}{5}$,
∴三棱锥A-BCH的体积VA-BCH=VH-ABC=$\frac{1}{3}×\frac{2}{5}×\frac{1}{2}×2×2$=$\frac{4}{15}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 非以上错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,4) | B. | (4,14) | C. | (2,14) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)>$\frac{f(2)}{2}$>$\frac{f(3)}{3}$ | B. | $\frac{f(1)}{2}$>$\frac{f(4)}{3}$>$\frac{f(9)}{4}$ | C. | f(1)<$\frac{f(2)}{2}$<$\frac{f(3)}{3}$ | D. | $\frac{f(1)}{2}$<$\frac{f(4)}{3}$<$\frac{f(9)}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4}$,$\frac{5}{8}$)∪($\frac{5}{4}$,+∞) | B. | (0,$\frac{1}{4}$]∪[$\frac{5}{8}$,1) | C. | ($\frac{1}{8}$,$\frac{1}{4}$)∪($\frac{5}{8}$,$\frac{5}{4}$) | D. | ($\frac{1}{8}$,$\frac{1}{4}$)∪($\frac{5}{8}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 分析法 | B. | 综合法 | ||
| C. | 综合法与分析法结合使用 | D. | 演绎法 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com