
| A. | f(1)>$\frac{f(2)}{2}$>$\frac{f(3)}{3}$ | B. | $\frac{f(1)}{2}$>$\frac{f(4)}{3}$>$\frac{f(9)}{4}$ | C. | f(1)<$\frac{f(2)}{2}$<$\frac{f(3)}{3}$ | D. | $\frac{f(1)}{2}$<$\frac{f(4)}{3}$<$\frac{f(9)}{4}$ |
分析 由题意构造函数g(x)=$\frac{f(x)}{\sqrt{x}+1}$,再由导函数的符号判断出函数g(x)的单调性,由函数g(x)的单调性即可得出正确选项.
解答 解:构造函数g(x)=$\frac{f(x)}{\sqrt{x}+1}$,
则g′(x)=$\frac{f′(x)•(\sqrt{x}+1)-f(x)•\frac{1}{2\sqrt{x}}}{(\sqrt{x}+1)^{2}}$=$\frac{2(x+\sqrt{x})f′(x)-f(x)}{2\sqrt{2}x•(\sqrt{x}+1)^{2}}$,
∵在(0,+∞)上的函数f(x)满足f(x)>2(x+$\sqrt{x}$)f′(x),
∴g′(x)<0,
∴g(x)=$\frac{f(x)}{\sqrt{x}+1}$在(0,+∞)上单调递减,
∴g(1)>g(4)>g(9),
∴$\frac{f(1)}{1+1}$>$\frac{f(4)}{2+1}$>$\frac{f(9)}{3+1}$,
∴$\frac{f(1)}{2}$>$\frac{f(4)}{3}$>$\frac{f(9)}{4}$,
故选:B
点评 本题考查了由条件构造函数和用导函数的符号判断函数的单调性,利用函数的单调性的关系对不等式进行判断.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
| 混凝土耐久性达标 | 混凝土耐久性不达标 | 总计 | |
| 使用淡化海砂 | 25 | t | 30 |
| 使用未经淡化海砂 | s | ||
| 总计 | 40 | 60 |
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{16}{5}$ | C. | 3 | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
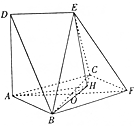 如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF,且∠DAF=90°.
如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF,且∠DAF=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=2(n+1)2 | B. | an=4(n+1) | C. | an=8n2 | D. | an=4n(n+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{5}{2}]$ | B. | (2,4) | C. | $(\frac{5}{2},4)$ | D. | (1,$\frac{5}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{9}{4}$,-2] | B. | [-1,0] | C. | (-∞,-2] | D. | (-$\frac{9}{4}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com