练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．给出下列一段推理：若一条直线平行于平面，则这条直线平行于平面内所有直线．已知直线a?平面α，直线b?平面α，且a∥α，所以a∥b．上述推理的结论不一定是正确的，其原因是（　　）
    A．大前提错误B．小前提错误C．推理形式错误D．非以上错误

    分析 分析该演绎推理的三段论，即可得出错误的原因是什么．

    解答 解：该演绎推理的大前提是：若直线平行于平面，则该直线平行于平面内所有直线；
    小前提是：已知直线a?平面α，直线b?平面α，且a∥α；
    结论是：a∥b；
    该结论是错误的，因为大前提是错误的，
    正确叙述是“若直线平行于平面，过该直线作平面与已知平面相交，则交线与该直线平行”．
    故选：A．

    点评 本题通过演绎推理的三段论叙述，考查了空间中线面垂直的性质定理的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．-150°的弧度数是（　　）
    A．-$\frac{5π}{6}$B．$\frac{4π}{3}$C．-$\frac{2π}{3}$D．-$\frac{3π}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若$P（A）=\frac{3}{4}$，$P（B）=\frac{1}{4}$，$P（AB）=\frac{1}{2}$，则P（B|A）=$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．函数f（x）=（x-3）ex在（0，+∞）上的零点个数是1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．某养殖场需定期购买饲料，已知该场每天需要饲料200千克，每千克饲料的价格为1.8元，饲料的保管费与其他费用平均每千克每天0.03元，购买饲料每次支付运费300元．
    （Ⅰ）求该养殖场多少天购买一次饲料才能使平均每天支付的总费用最少；
    （Ⅱ）若提供饲料的公司规定，当一次购买饲料不少于5吨时，其价格可享受八五折优惠（即为原价的85%）．问：为使该养殖场平均每天支付的总费用最少，该场是否应考虑利用此优惠条件？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．2017年4月14日，某财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象．为了研究使用淡化海砂与混凝土耐久性是否达标有关，某大学实验室随机抽取了60个样本，得到了相关数据如表：
    混凝土耐久性达标混凝土耐久性不达标总计
    使用淡化海砂25t30
    使用未经淡化海砂s
    总计4060
    （Ⅰ）根据表中数据，求出s，t的值；
    （Ⅱ）利用独立性检验的方法判断，能否在犯错误的概率不超过1%的前提下认为使用淡化海砂与混凝土耐久性是否达标有关？
    参考数据：
    P（K2≥k0）0.1000.0500.0250.0100.001
    k02.7063.8415.0246.63510.828
    参考公式：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．$\frac{i}{{\sqrt{7}+3i}}$=（　　）
    A．$\frac{3}{16}-\frac{{\sqrt{7}}}{16}i$B．$\frac{3}{16}+\frac{{\sqrt{7}}}{16}i$C．$-\frac{3}{16}+\frac{{\sqrt{7}}}{16}i$D．$-\frac{3}{16}-\frac{{\sqrt{7}}}{16}i$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知命题p：?x∈R，x2+ax+a2≥0（a∈R），命题q：$?{x_0}∈{N^*}$，$2x_0^2-1≤0$，则下列命题中为真命题的是（　　）
    A．p∧qB．p∨qC．（?p）∨qD．（?p）∧（?q）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

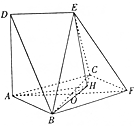    18．如图，边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直，AF∩BC=O，DE=$\sqrt{2}$，ED∥AF，且∠DAF=90°．
    （1）求证：DE⊥平面BCE；
    （2）过O作OH⊥平面BEF，垂足为H，求三棱锥A-BCH的体积．

    查看答案和解析>>

    同步练习册答案