
���� �ɶ�$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-2\overrightarrow{b}|$����ƽ����Ȼ����������������㣬��ɵó�${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}={\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}$������������$\overrightarrow{a}��\overrightarrow{b}$Ϊ��λ�����������$\overrightarrow{a}•\overrightarrow{b}$��ֵ��
��� �⣺������������$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-2\overrightarrow{b}|$�ã�
$��\overrightarrow{a}+\overrightarrow{b}��^{2}=��\overrightarrow{a}-2\overrightarrow{b}��^{2}$��
��${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}={\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}$��
��$1+2\overrightarrow{a}•\overrightarrow{b}+1=1-4\overrightarrow{a}•\overrightarrow{b}+4$��
��$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{2}$��
�ʴ�Ϊ��$\frac{1}{2}$��
���� ���鵥λ�����ĸ���Լ������������㼰���㹫ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
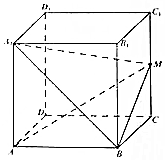 ��֪�ⳤΪ1��������ABCD-A1B1C1D1�У�M����CC1���е㣬������A1-ABM�����Ϊ$\frac{1}{6}$��
��֪�ⳤΪ1��������ABCD-A1B1C1D1�У�M����CC1���е㣬������A1-ABM�����Ϊ$\frac{1}{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
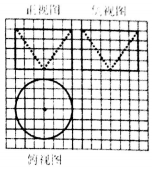 ��ͼ��ʾ������ֽ��С�����εı߳�Ϊ1������������ijһ���ϸǼ����������ͼ����ü�����ı�������ڣ�������
��ͼ��ʾ������ֽ��С�����εı߳�Ϊ1������������ijһ���ϸǼ����������ͼ����ü�����ı�������ڣ�������| A�� | 39�� | B�� | 48�� | C�� | 57�� | D�� | 63�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱ��y=-3x�� | B�� | ��ֱ��y=3x�� | C�� | ��ֱ��y=-4x�� | D�� | ��ֱ��y=4x�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com