
分析 (Ⅰ)设出圆的一般方程,利用待定系数法求圆C的方程;
(Ⅱ)求出|AB|,P到AB距离的最大值为d+r,即可求△PAB的面积的最大值.
解答 解:(Ⅰ)设所求圆的方程为x2+y2+Dx+Ey+F=0 …(1分)
依题意得$\left\{\begin{array}{l}{1-E+F=0}\\{25+4D+3E+F=0}\\{3•(-\frac{D}{2})+(-\frac{E}{2})-15=0}\end{array}\right.$ …(2分)
解得D=-12,E=6,F=5 …(5分)
∴所求圆的方程是x2+y2-12x+6y+5=0 …(6分)
(Ⅱ)|AB|=$\sqrt{16+16}$=4$\sqrt{2}$,…(7分)
由已知知直线AB的方程为x-y-1=0 …(8分)
所以圆心C(6,-3)到AB的距离为d=4$\sqrt{2}$ …(9分)
P到AB距离的最大值为d+r=4$\sqrt{2}$+2$\sqrt{10}$ …(11分)
所以△PAB面积的最大值为$\frac{1}{2}×4\sqrt{2}×(4\sqrt{2}+2\sqrt{10})$=16+8$\sqrt{5}$ …(12分)
点评 本题考查圆的方程,考查三角形面积的计算,考查系数分析解决问题的能力,比较基础.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:选择题

| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{5\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{10}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{5}$ | D. | -$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
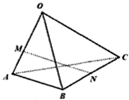 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )| A. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com