
分析 由f(3x)的定义域求出f(x)的定义域,然后由$lo{g}_{\frac{1}{3}}$(x+1)在f(x)的定义域内求解对数不等式得答案.
解答 解:∵f(3x)的定义域是[1,3],即1≤x≤3,
得3x∈[3,27],
∴函数f(x)的定义域为[3,27],
再由3≤$lo{g}_{\frac{1}{3}}$(x+1)≤27,得-27≤log3(x+1)≤-3,
即3-27≤x+1≤3-3,∴$\frac{1}{{3}^{27}}-1≤x≤\frac{1}{27}-1$.
∴f[$lo{g}_{\frac{1}{3}}$(x+1)]的定义域为[$\frac{1}{{3}^{27}}-1,\frac{1}{27}-1$].
点评 本题考查函数的定义域及其求法,关键是掌握该类问题的解决方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | (x-1)2+y2=1 | C. | x2-y2=1 | D. | $\frac{x^2}{2}+{y^2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
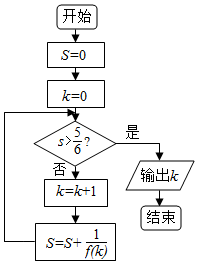
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
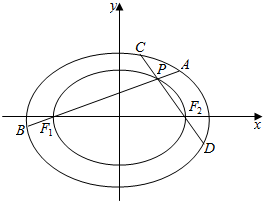 如图,已知点F1,F2是椭圆C1:$\frac{{x}^{2}}{2}$+y2=1的两个焦点,椭圆C2:$\frac{{x}^{2}}{2}$+y2=λ经过点F1,F2,点P是椭圆C2上异于F1,F2的任意一点,直线PF1和PF2与椭圆C1的交点分别是A,B和C,D,设AB、CD的斜率为k,k′.
如图,已知点F1,F2是椭圆C1:$\frac{{x}^{2}}{2}$+y2=1的两个焦点,椭圆C2:$\frac{{x}^{2}}{2}$+y2=λ经过点F1,F2,点P是椭圆C2上异于F1,F2的任意一点,直线PF1和PF2与椭圆C1的交点分别是A,B和C,D,设AB、CD的斜率为k,k′.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com