Question

12．直线l₁与l₂是圆x²+y²=1的两条切线，若l₁与l₂的交点为（1，2），则l₁与l₂的夹角的正切值等于$\frac{4}{3}$．

Answer 1

分析 作出对应的图象，设∠OBA=θ，求出tanθ，利用正切的倍角公式进行求解即可．

解答 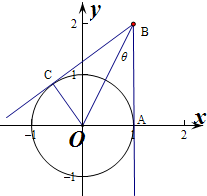解：作出对应的图象如图：
则B（1，2），A（1，0），
设∠OBA=θ，
则tanθ=$\frac{OA}{AB}=\frac{1}{2}$，
则l₁与l₂的夹角为∠ABC=2θ，
则tan∠ABC=tan2θ=$\frac{2tanθ}{1-ta{n}^{2}θ}$=$\frac{2×\frac{1}{2}}{1-（\frac{1}{2}）^{2}}=\frac{1}{1-\frac{1}{4}}$=$\frac{4}{3}$，
故答案为：$\frac{4}{3}$

点评 本题主要考查三角函数值的求解，根据直线和圆相切的位置关系，求出tanθ，利用正切的倍角公式是解决本题的关键．