
【题目】在进行一项掷骰子放球游戏中,规定:若掷出1点,甲盒中放一球;若掷出2点或3点,乙盒中放一球;若掷出4点或5点或6点,丙盒中放一球,前后共掷3次,设![]() 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.
(Ⅰ)求![]() 的概率;
的概率;
(Ⅱ)记![]() 求随机变量
求随机变量![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】某高科技公司研究开发了一种新产品,生产这种新产品的每天固定成木为30000元,每生产x件,需另投入成本为t元, 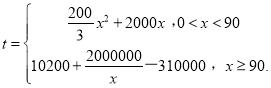 ,每件产品售价为10000元.(该新产品在市场上供不应求可全部卖完.)
,每件产品售价为10000元.(该新产品在市场上供不应求可全部卖完.)
(1)写出每天利润y关于每天产量x的函数解析式;
(2)当每天产量为多少件时,该公司在这一新产品的生产中每天所获利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据悉,2017年教育机器人全球市场规模已达到8.19亿美元,中国占据全球市场份额10.8%.通过简单随机抽样得到40家中国机器人制造企业,下图是40家企业机器人的产值频率分布直方图.

(1)求![]() 的值;
的值;
(2)在上述抽取的40个企业中任取3个,抽到产值小于500万元的企业不超过两个的概率是多少?
(3)在上述抽取的40个企业中任取2个,设![]() 为产值不超过500万元的企业个数减去超过500万元的企业个数的差值,求
为产值不超过500万元的企业个数减去超过500万元的企业个数的差值,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,且取相等的单位长度,建立平面直角坐标系,直线
轴的正半轴,且取相等的单位长度,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是 (
(![]() 是参数),设点
是参数),设点![]() .
.
(Ⅰ)将曲线![]() 的极坐标方程化为直角坐标方程,将直线
的极坐标方程化为直角坐标方程,将直线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
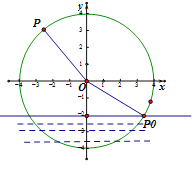
【题目】一半径为![]() 的水轮,水轮圆心
的水轮,水轮圆心![]() 距离水面2
距离水面2![]() ,已知水轮每分钟转动(按逆时针方向)3圈,当水轮上点
,已知水轮每分钟转动(按逆时针方向)3圈,当水轮上点![]() 从水中浮现时开始计时,即从图中点
从水中浮现时开始计时,即从图中点![]() 开始计算时间.
开始计算时间.
(1)当![]() 秒时点
秒时点![]() 离水面的高度_________;
离水面的高度_________;
(2)将点![]() 距离水面的高度
距离水面的高度![]() (单位:
(单位: ![]() )表示为时间
)表示为时间![]() (单位:
(单位: ![]() )的函数,则此函数表达式为_______________ .
)的函数,则此函数表达式为_______________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部![]() 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 |
|
|
未参加演讲社团 |
|
|
(1)从该班随机选![]() 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的![]() 名同学中,有5名男同学
名同学中,有5名男同学![]()
![]() 名女同学
名女同学![]() 现从这
现从这![]() 名男同学和
名男同学和![]() 名女同学中各随机选
名女同学中各随机选![]() 人,求
人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com