
| A. | $({-\frac{1}{4},0})$ | B. | $({0,\frac{1}{4}})$ | C. | $({\frac{1}{4},\frac{1}{2}})$ | D. | $({\frac{1}{2},1})$ |
分析 由题意可得b=6lna-2a2,d=2c+6;而(a-c)2+(b-d)2的几何意义是点(a,b)与点(c,d)的距离的平方;从而化为求函数y=6lnx-2x2上的点到直线y=2x+6的距离的平方的最小值,从而由导数求切点,从而求出m,再由函数零点的判定定理求解即可.
解答 解:∵(b+2a2-6lna)2+|2c-d+6|=0,
∴b+2a2-6lna=0,2c-d+6=0;
即b=6lna-2a2,d=2c+6;
而(a-c)2+(b-d)2的几何意义是点(a,b)与点(c,d)的距离的平方;
故m是函数y=6lnx-2x2上的点到直线y=2x+6的距离的平方的最小值;
令y′=$\frac{6}{x}$-4x=2得,x=1;
故切点坐标为(1,-2);
故m=$(\frac{|2+6-(-2)|}{\sqrt{{2}^{2}+1}})^{2}$=20;
故函数f(x)=ex+4x-3;
而f($\frac{1}{4}$)=$\root{4}{e}$+1-3=$\root{4}{e}$-2<0,
f($\frac{1}{2}$)=$\sqrt{e}$+2-3=$\sqrt{e}$-1>0;
故f($\frac{1}{4}$)f($\frac{1}{2}$)<0;
故函数f(x)=ex+$\frac{1}{5}$mx-3零点所在的区间为($\frac{1}{4}$,$\frac{1}{2}$);
故选:C.
点评 本题考查了导数的几何意义的应用及函数的应用,同时考查了函数零点的判定定理的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -$\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $2\sqrt{5}$ | C. | 20 | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 82 | 82 | 79 | 95 | 87 |
| 乙 | 95 | 75 | 80 | 90 | 85 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
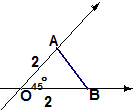
| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com