
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
分析 设x=rcosα,y=rsinα,(r>0),α∈[0,2π).代入x2-2xy+3y2=4,可得$\frac{1}{{x}^{2}+{y}^{2}}$=$\frac{1}{{r}^{2}}$=$\frac{1}{4}$(cos2α-2cosαsinα+3sin2α)=$\frac{1}{4}$(2-cos2α-sin2α),再利用和差公式、三角函数的单调性值域即可得出.
解答 解:设x=rcosα,y=rsinα,(r>0),α∈[0,2π).
∵x2-2xy+3y2=4,
∴r2cos2α-2rcosαrsinα+3r2sin2α=4,
∴r2(cos2α-2cosαsinα+3sin2α)=4,
∴$\frac{1}{{x}^{2}+{y}^{2}}$=$\frac{1}{{r}^{2}}$=$\frac{1}{4}$(cos2α-2cosαsinα+3sin2α)=$\frac{1}{4}$(1+2sin2α-sin2α)=$\frac{1}{4}$(2-cos2α-sin2α)$\frac{1}{4}$$[2-\sqrt{2}sin(2α+\frac{π}{4})]$∈$[\frac{2-\sqrt{2}}{4},\frac{2+\sqrt{2}}{4}]$,
∴$\frac{1}{{x}^{2}+{y}^{2}}$最大值与最小值的和=$\frac{2-\sqrt{2}}{4}$+$\frac{2+\sqrt{2}}{4}$=1.
故选:B.
点评 本题考查了同角三角函数基本关系式、和差公式与倍角公式、三角函数的单调性值域,考查了换元方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
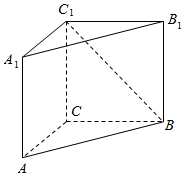 三棱柱ABC-A1B1C1的侧棱垂直底面,AC⊥BC,AC=BC=4,AA1=4.
三棱柱ABC-A1B1C1的侧棱垂直底面,AC⊥BC,AC=BC=4,AA1=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-3y-1=0 | B. | x+3y-2=0 | C. | 2x+3y=0 | D. | 3x-2y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 终边在x轴负半轴上的角是零角 | B. | 第二象限角一定是钝角 | ||
| C. | 第四象限角一定是负角 | D. | 若β=α+k•360°(k∈Z),则α与β终边相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com