
分析 (1)∠AOB=120°,用底面半径表示出AB和SC,根据面积求出底面半径,利用二面角得出圆锥额高SO,根据等积法求出O到平面SAB的距离;
(2)根据圆锥的高与底面半径的比值求出线面角.
解答 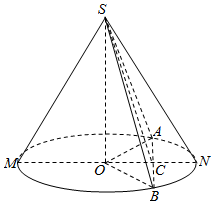 解:(1)∵A、B分底面圆周为1:2的圆弧,∴∠AOB=120°,
解:(1)∵A、B分底面圆周为1:2的圆弧,∴∠AOB=120°,
过O作OC⊥AB于C,连结SC,则∠SCO=60°,
设底面半径OA=r,则OC=$\frac{1}{2}r$,AB=2$\sqrt{{r}^{2}-\frac{{r}^{2}}{4}}$=$\sqrt{3}r$,SC=2OC=r,∴SO=$\frac{\sqrt{3}}{2}r$,
∵S△SAB=$\frac{1}{2}AB×SC$=$\frac{1}{2}×\sqrt{3}r×r$=24$\sqrt{3}$,∴r=4$\sqrt{3}$.∴SO=6,
设圆心O到平面SAB的距离为h,
则V棱锥S-OAB=$\frac{1}{3}{S}_{△OAB}•SO$=$\frac{1}{3}{S}_{△SAB}•h$.
∴h=$\frac{{S}_{△OAB}•SO}{{S}_{△SAB}}$=$\frac{\frac{1}{2}×(4\sqrt{3})^{2}×sin120°×6}{24\sqrt{3}}$=3.
即底面圆心到平面SAB的距离为3.
(2)在Rt△SOB中,tan∠SBO=$\frac{SO}{OB}$=$\frac{6}{4\sqrt{3}}$=$\frac{\sqrt{3}}{2}$.
∴∠SBO=arctan$\frac{\sqrt{3}}{2}$.
即母线与底面所成角的大小为arctan$\frac{\sqrt{3}}{2}$.
点评 本题考查了圆锥的结构特征,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在等腰直角三角形ABC,∠C=90°,点D在线段AB上,且AD=$\frac{1}{3}$AB,延长线段CD至点E,使DE=CD,求cos∠CBE.
如图,在等腰直角三角形ABC,∠C=90°,点D在线段AB上,且AD=$\frac{1}{3}$AB,延长线段CD至点E,使DE=CD,求cos∠CBE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
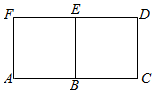 如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出:
如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
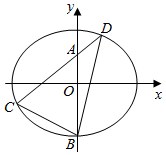 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
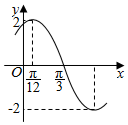 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)的图象上所有点向右平移$\frac{π}{12}$个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)的图象上所有点向右平移$\frac{π}{12}$个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( )| A. | $[kπ-\frac{π}{3},kπ+\frac{π}{6}]$,k∈Z | B. | $[kπ+\frac{π}{6},kπ+\frac{2π}{3}]$,k∈Z | ||
| C. | $[kπ-\frac{π}{12},kπ+\frac{π}{12}]$,k∈Z | D. | $[kπ-\frac{7π}{12},kπ-\frac{π}{12}]$,k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com