
分析 先确定概率类型是几何概型中的面积类型,再设甲到x点,乙到y点,建立甲先到,乙先到满足的条件,再画出并求解0<x<24,0<y<24可行域面积,再求出满足条件的可行域面积,由此求出概率.
解答 解:设甲、乙两车达泊位的时刻分别为x,y.则作出如图所示的区域: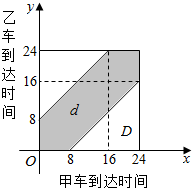
区域D的面积S1=242,
区域d的面积S2=242-162.
∴P=$\frac{d的面积}{D的面积}$=$\frac{{24}^{2}{-16}^{2}}{{24}^{2}}$=$\frac{5}{9}$.
即两车中有一车在停泊位时另一车必须等待的概率为$\frac{5}{9}$.
点评 本题主要考查了建模与解模能力,解答时应利用线性规划作出事件对应的平面区域,再利用几何概型概率公式求出对应事件的概率.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $m<\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}<m<\frac{{\sqrt{2}}}{2}$ | C. | $m<-\frac{{\sqrt{2}}}{2}$ | D. | $m>\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
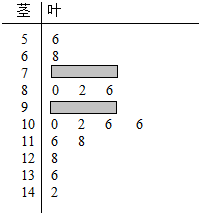 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com