练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．$\overrightarrow a$=（-1，-5，-2），$\overrightarrow b$=（x，2，x+2），若$\overrightarrow a⊥\overrightarrow b$，则x=（　　）
    A．0B．-6C．$-\frac{14}{3}$D．±6

    分析 利用向量垂直的性质直接求解．

    解答 解：∵$\overrightarrow a$=（-1，-5，-2），$\overrightarrow b$=（x，2，x+2），$\overrightarrow a⊥\overrightarrow b$，
    ∴$\overrightarrow{a}•\overrightarrow{b}$=-x-10-2x-4=0，
    解得x=-$\frac{14}{3}$．
    故选：C．

    点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意向量垂直的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．如图，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左右焦点为F1，F2，P是椭圆上一点，M在PF1上，$\overrightarrow{{F}_{1}M}$=2$\overrightarrow{MP}$，PO⊥F2M．则椭圆离心率e的取值范围是（　　）
    A．$（{0，\frac{{\sqrt{2}}}{2}}）$B．$（{\frac{{\sqrt{2}}}{2}，1}）$C．$（{0，\frac{1}{2}}）$D．$（{\frac{1}{2}，1}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．某实心钢质工件的三视图如图所示，其中侧视图为等腰三角形，俯视图是一个半径为3的半圆，现将该工件切削加工成一个球体，则该球体的最大体积为（　　）
    A．$\frac{4π}{3}$B．$\frac{2π}{3}$C．πD．$\frac{3π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．运行如图所示的程序框图，当输入实数x的值为-3时，输出的函数值为12，当输入实数x的值为1时，输出的函数值为2．
    （1）求函数f（x）的解析式；
    （2）当输出结果为80时，求输入的x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知集合A={x|$\frac{3}{x}$＜1}，集合B={y|y=t-2$\sqrt{t-3}$}，则A∩B={x|x＞3}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知抛物线y2=2px（p＞0）的准线和圆x2+y2+6x+8=0相切，则实数p=（　　）
    A．p=4B．p=8C．p=4或p=8D．p=2或p=4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

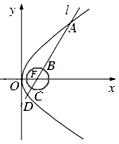    11．如图，已知抛物线y2=4x的焦点为F，直线l过F且依次交抛物线及圆（x-1）2+y2=$\frac{1}{4}$于点A，B，C，D四点，则9|AB|+4|CD|的最小值为$\frac{37}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知双曲线的焦点到渐进线的距离等于实半轴长，则该双曲线的离心率为（　　）
    A．$\frac{{\sqrt{5}+1}}{2}$B．2C．$\sqrt{2}$D．$2\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知数列1，$\sqrt{3}$，$\sqrt{5}$，$\sqrt{7}$，…，$\sqrt{2n-1}$，…则3$\sqrt{5}$是它的第23项．

    查看答案和解析>>

    同步练习册答案