
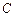 :
:
 上的一动点
上的一动点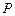 到右焦点的最短距离为
到右焦点的最短距离为 ,且右焦点到右准线的距离等于短半轴的长.
,且右焦点到右准线的距离等于短半轴的长.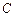 的方程;
的方程; (
( ,
,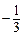 )的动直线
)的动直线 交椭圆
交椭圆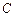 于
于 、
、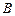 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得无论
,使得无论 如何转动,以
如何转动,以
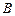 为直径的圆恒过定点
为直径的圆恒过定点 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. ,则由题设可知
,则由题设可知 ,解此方程组得
,解此方程组得 ,
, . 所以椭圆C的方程是
. 所以椭圆C的方程是 . ………5分
. ………5分 ,
, .
. ,则
,则
 及
及


 ……9分
……9分 恒成立时,以AB为直径的圆恒过定点T,
恒成立时,以AB为直径的圆恒过定点T, 解得
解得
 也过点T(0,1).
也过点T(0,1).
 ……7分
……7分 解得
解得 .
. ,
, ,代入椭圆方程,并整理,得
,代入椭圆方程,并整理,得
 ,则
,则 ……10分
……10分 ,
,

 ,即以AB为直径的圆恒过定点T(0,1).
,即以AB为直径的圆恒过定点T(0,1). 

科目:高中数学 来源:不详 题型:解答题

 时,求直线l的方程;
时,求直线l的方程; 为定值.
为定值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
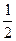 (O为坐标原点).
(O为坐标原点). 轴不垂直时,
轴不垂直时, 点C,使得△ABC为等边三角形,求a
点C,使得△ABC为等边三角形,求a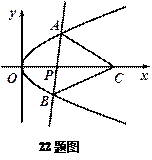
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点
作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点 ,若
,若 是等腰三角形,则双曲线的离心率为( )
是等腰三角形,则双曲线的离心率为( )A. | B. |
C. | D. |

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 上异于一条直径两个端点的任意一点与这条直径两个端点连线的斜率存在,则这两条直线的斜率乘积为定值-1。写出该定理在有心曲线
上异于一条直径两个端点的任意一点与这条直径两个端点连线的斜率存在,则这两条直线的斜率乘积为定值-1。写出该定理在有心曲线 中的推广 。
中的推广 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com