
分析 (1)由题意所含白球的个数X的可能取值为0,1,2,分别说明随机变量所取的值表示的随机试验的结果即可.
(2)由题意ξ的可能取值为3,4,5,分别说明随机变量所取的值表示的随机试验的结果即可.
解答 解:(1)一个袋中装有2个白球和5个黑球,从中任取3个,
其中所含白球的个数X的可能取值为0,1,2,
X=0表示取到3个黑球;
X=1表示取到2个黑球1个白球;
X=2表示取到1个黑球2个白球.
(2)∵一个袋中装有5个同样大小的球,编号为1,2,3,4,5.
现从该袋内随机取出3个球,被取出的球的最大号码数为ξ,
∴ξ的可能取值为3,4,5,
ξ=3表示取到的三个球编号分别为1,2,3;
ξ=4表示取到4号球,且在编号为1,2,3的三个球中取到2个;
ξ=5表示取到5号球,且编号为1,2,3,4的四个球中取到2个.
点评 本题考查离散型随机变量的可能取值的求法,并说明随机变量所取的值表示的随机试验的结果,是基础题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 13 | C. | 12或13 | D. | 13或14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 其图象关于直线x=-$\frac{π}{4}$对称 | B. | 函数g(x)是奇函数 | ||
| C. | 在[$\frac{π}{4}$,$\frac{π}{2}$]上是增函数 | D. | x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,函数g(x)的值域是[-2,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=1.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
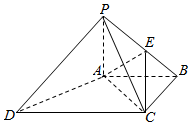 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com