考点:用空间向量求平面间的夹角,平面与平面垂直的判定,与二面角有关的立体几何综合题,点、线、面间的距离计算
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(1)由已知条件推导出AB⊥BC,建立直角坐标系,利用向量法能求出平面ADC
1⊥面A
1ACC
1.
(2)求出平面ADC
1的法向量
,设点B到平面的距离ADC
1为d,由d=
能求出结果.
(3)分别求出平面ABC的法向量和平面ADC
1的法向量,利用向量法能求出平面ADC
1与平面ABC所成的二面角的大小.
解答:
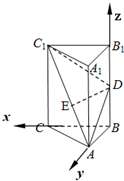
(1)证明:∵
A1A=AC=AB,AB=BC=a,
∴AB
2+BC
2=AC
2,由勾股定理知AB⊥BC,
则如图所示建立直角坐标系,由题意知坐标分别为:
B(0,0,0),A(0,a,0),C(a,0,0),B1(0,0,a),A1(0,a,a)C1(a,0,a)∵D
1,E分别是BB
1,AC
1之中点.
∴
D(0,0,a),E(,,a),
∴
=(,,0),
=(0,0,a),
=(a,-a,a),
∵
•=0,
•=0,
∴DE⊥AC
1,DE⊥CC
1,
∵AC∩CC
1=C
1,∴DE⊥面A
1ACC
1,
∵DE?平面ADC
1,∴平面ADC
1⊥面A
1ACC
1.…(4分)
(2)解:设平面ADC
1的法向量
=(x1,y1,z1),
且
=(0,-a,a),
=(a,-a.a),
∴
| | •=-ay1+az1=0 | | •=ax1-ay1+az1=0 |
| |
,
∴
=(-
,
,1),又∵
=(0,a,0),
设点B到平面的距离ADC
1为d,
则d=
=
=
a.
∴点B到平面ADC
1的距离为
a.…(8分)
(3)解:∵平面ABC的法向量为
=(0,0,1),
平面ADC
1的法向量
=(-
,
,1),
∴cos<
,
>=
=
,
平面ADC
1与平面ABC所成的二面角为
.…(12分)
点评:本题考查平面与平面垂直的证明,考查点到平面的距离的求法,考查平面与平面所成二面角的求法,解题时要注意向量法的合理运用.

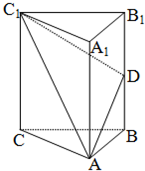 如图,在直三棱柱ABC-A1B1C1中,A1A=AC=
如图,在直三棱柱ABC-A1B1C1中,A1A=AC= (1)证明:∵A1A=AC=
(1)证明:∵A1A=AC=

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案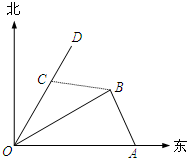 如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.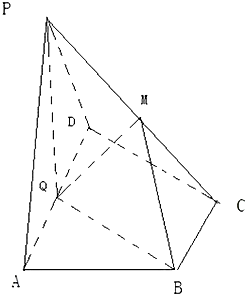 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=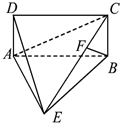 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.