Question

14．如图，在△APC中，点B是AC中点，AC=2，∠APB=90°，∠BPC=45°，则$\overrightarrow{PA}$•$\overrightarrow{PC}$=-$\frac{4}{5}$．

Answer 1

分析 由已知可得$\overrightarrow{PA}$•$\overrightarrow{PC}$=$\overrightarrow{PA}$•（2$\overrightarrow{PB}$-$\overrightarrow{PA}$）=2$\overrightarrow{PA}$•$\overrightarrow{PB}$-$\overrightarrow{PA}$²=-$\overrightarrow{PA}$²=-|$\overrightarrow{PA}$|²，根据三角形外角平分线定理及勾股定理求出AP长，可得答案．

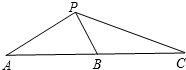
解答 解：∵在△APC中，点B是AC中点，
∴$\overrightarrow{PA}$+$\overrightarrow{PC}$=2$\overrightarrow{PB}$，即$\overrightarrow{PC}$=2$\overrightarrow{PB}$-$\overrightarrow{PA}$，
故$\overrightarrow{PA}$•$\overrightarrow{PC}$=$\overrightarrow{PA}$•（2$\overrightarrow{PB}$-$\overrightarrow{PA}$）=2$\overrightarrow{PA}$•$\overrightarrow{PB}$-$\overrightarrow{PA}$²，
∵∠APB=90°，
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$=0，
即$\overrightarrow{PA}$•$\overrightarrow{PC}$=-$\overrightarrow{PA}$²=-|$\overrightarrow{PA}$|²，
∵∠BPC=45°，AC=2，
由三角形外角平分线定理得：PA：PB=AC：BC，
故AP=2PB，AB=1，
解得：AP=$\frac{2\sqrt{5}}{5}$，
故$\overrightarrow{PA}$•$\overrightarrow{PC}$=-$\frac{4}{5}$，
故答案为：-$\frac{4}{5}$

点评 本题考查的知识点是平面向量的数量积运算，平面向量在平面几何中的应用，难度中档．