
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)求出a的值,求出函数f(x)的导数,根据函数的单调性证明即可.
解答 解:(1)f'(x)=ex(ax2+x+1)+ex(2ax+1)=$a{e^x}(x+\frac{1}{a})(x+2)$,
当$a=\frac{1}{2}$时,$f'(x)=\frac{1}{2}{e^x}{(x+2)^2}≥0$,f(x)在R上单调递增;
当$0<a<\frac{1}{2}$时,f'(x)>0,解得x>-2或$x<-\frac{1}{a}$;f'(x)<0,解得$-\frac{1}{a}<x<-2$,
故函数f(x)在$(-∞,-\frac{1}{a})$和(-2,+∞)上单调递增,在$(-\frac{1}{a},-2)$上单调递减.
当$a>\frac{1}{2}$时,f'(x)>0,解得$x>-\frac{1}{a}$或x<-2;f'(x)<0,解得$-2<x<-\frac{1}{a}$,
故函数f(x)在(-∞,-2)和$(-\frac{1}{a},+∞)$上单调递增,在$(-2,-\frac{1}{a})$上单调递减.
所以当$a=\frac{1}{2}$时,f(x)的单调递增区间是(-∞,+∞);
当$0<a<\frac{1}{2}$时,f(x)的单调递增区间是$(-∞,-\frac{1}{a})$和(-2,+∞),单调递减区间是$(-\frac{1}{a},-2)$;
当$a>\frac{1}{2}$时,f(x)的单调递增区间是(-∞,-2)和$(-\frac{1}{a},+∞)$,单调递减区间是$(-2,-\frac{1}{a})$.
(2)证明:∵x=1时,f(x)有极值,∴f'(x)=3e(a+1)=0,∴a=-1,
∴f(x)=ex(-x2+x+1),f'(x)=-ex(x-1)(x+2),
由f'(x)>0,得-2<x<1,∴f(x)在[-2,1]上单调递增.
∵$θ∈[{0,\frac{π}{2}}]$,∴sinθ,cosθ∈[0,1],
∴|f(cosθ)-f(sinθ)|≤f(1)-f(0)=e-1<2.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查转化思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
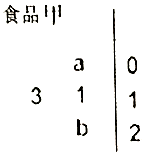 为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )
为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | 3 | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com