Question

3．高为$\sqrt{2}$的四棱锥S-ABCD的底面是边长为1的正方形，点S、A、B、C、D均同一球面上，底面ABCD的中心为O₁，球心O到底面ABCD的距离为$\frac{{\sqrt{2}}}{2}$，则异面直线SO₁与AB所成角的余弦值的范围为[0，$\frac{\sqrt{10}}{10}$]．

Answer 1

分析 由题意可知ABCD是小圆，对角线长为$\sqrt{2}$，四棱锥的高为$\sqrt{2}$，推出高就是四棱锥的一条侧棱，最长的侧棱就是球的直径，然后利用勾股定理求出底面ABCD的中心O₁与顶点S之间的距离，取BC的中点M，连接SM，O1M，∠SO₁M或补角是异面直线SO₁与AB所成的角，运用余弦定理即可求得．

解答 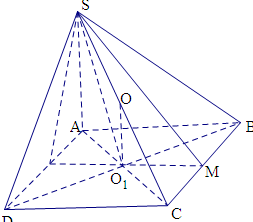解：由题意可知ABCD是正方形，对角线长为$\sqrt{2}$，四棱锥的高为$\sqrt{2}$，球心O到底面ABCD的距离为$\frac{{\sqrt{2}}}{2}$，所以点S，A，B，C，D均在半径为1的同一球面上，球的直径为2，所以四棱锥的一条侧棱垂直底面，最长的侧棱就是直径，
所以底面ABCD的中心O₁与顶点S之间的距离为：$\sqrt{2+\frac{1}{2}}$=$\frac{\sqrt{10}}{2}$．
取BC的中点M，连接SM，O₁M，
∠SO₁M或补角是异面直线SO₁与AB所成的角，
SO₁=$\frac{\sqrt{10}}{2}$，O₁M=$\frac{1}{2}$，SM=$\sqrt{2+1+\frac{1}{4}}$=$\frac{\sqrt{13}}{2}$，
由余弦定理得cos∠SO₁M=$\frac{\frac{10}{4}+\frac{1}{4}-\frac{13}{4}}{2×\frac{\sqrt{10}}{2}×\frac{1}{2}}$=-$\frac{\sqrt{10}}{10}$
故异面直线SO₁与AB所成的最小角的余弦值为$\frac{\sqrt{10}}{10}$，
∴异面直线SO₁与AB所成角的余弦值的范围为[0，$\frac{\sqrt{10}}{10}$]．
故答案为[0，$\frac{\sqrt{10}}{10}$]．

点评 本题是中档题，考查球的内接多面体的知识，能够正确推出四棱锥的一条侧棱垂直底面，最长的侧棱就是直径是本题的关键，考查空间异面直线所成的角，以及逻辑推理能力，计算能力．