
分析 (1)求出f(x)的解析式,将f(x)以及f(-x)读法解析式代入不等式,求出不等式的解集即可;
(2)求出f(x)-f(a),根据绝对值的性质证明即可.
解答 (1)解:函数f(x)=x2+bx+c的顶点为(1,-1),
故$\left\{\begin{array}{l}{-\frac{b}{2}=1}\\{\frac{4c{-b}^{2}}{4}=-1}\end{array}\right.$,解得:b=-2,c=0,
故f(x)=x2-2x,
则不等式为|x2+2x|+|x2-2x|≥4|x|,
∵|x2+2x|+|x2-2x|≥|(x2+2x)-(x2-2x)|=|4x|=4|x|,
当且仅当x∈[-2,2]时取等号,
所以不等式恒成立,解集为x∈R.
(2)证明:|f(x)-f(a)|=|x2-2x-a2+2a|=|(x-a)(x+a-2)|
=|x-a||x+a-2|$<\frac{1}{2}|x+a-2|=\frac{1}{2}|x-a+2a-2|≤\frac{1}{2}(|x-a|+2|a|+2)$
$<\frac{1}{2}({\frac{1}{2}+2|a|+2})=|a|+\frac{5}{4}$.
点评 本题考查了二次函数的性质,考查解不等式问题以及不等式的证明,是一道中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (3,-3) | B. | $(-\sqrt{3},3)$ | C. | $(\sqrt{3},-3)$ | D. | $(3,-\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过圆心 | B. | 相交而不过圆心 | C. | 相切 | D. | 相离 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
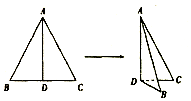 如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )
如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )| A. | $\frac{13}{2}π$ | B. | $\frac{13}{3}π$ | C. | $\frac{{13\sqrt{3}}}{2}π$ | D. | $\frac{{13\sqrt{3}}}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com