
分析 (1)先化简函数,再求f(x)的单调递增区间;
(2)先求出A,求出bc的最大值,再求△ABC的最大面积.
解答 解:(1)$f(x)=sinx•sin({x+\frac{π}{6}})=sinx•({\frac{{\sqrt{3}}}{2}sinx+\frac{1}{2}cosx})=\frac{{\sqrt{3}}}{2}{sin^2}x+\frac{1}{2}sinxcosx$
=$\frac{1-cos2x}{2}×\frac{{\sqrt{3}}}{2}+\frac{1}{2}sin2x×\frac{1}{2}=\frac{1}{4}sin2x-\frac{{\sqrt{3}}}{4}cos2x+\frac{{\sqrt{3}}}{4}=\frac{1}{2}sin({2x-\frac{π}{3}})+\frac{{\sqrt{3}}}{4}$,
令$-\frac{π}{2}+2kπ≤2x-\frac{π}{3}≤\frac{π}{2}+2kπ({k∈Z})$,
得$-\frac{π}{12}+kπ≤x≤\frac{5π}{12}+kπ({k∈Z})$.
∴f(x)的单调递增区间为$[{-\frac{π}{12}+kπ,\frac{5π}{12}+kπ}]({k∈Z})$.
(2)由$f(A)=\frac{{\sqrt{3}}}{4}$,得$\frac{1}{2}sin({2A-\frac{π}{3}})+\frac{{\sqrt{3}}}{4}=\frac{{\sqrt{3}}}{4}$,
∴$sin({2A-\frac{π}{3}})=0$,∴$2A-\frac{π}{3}=kπ,k∈Z$,∴$A=\frac{π}{6}+\frac{kπ}{2},k∈Z$,
又∵$0<A<\frac{π}{2}$,∴$A=\frac{π}{6}$,
∴$4={b^2}+{c^2}-2bc•cos\frac{π}{6}≥2bc-2bc•\frac{{\sqrt{3}}}{2}=({2-\sqrt{3}})bc$.
∴$bc≤\frac{4}{{2-\sqrt{3}}}=4({2+\sqrt{3}})$,当且仅当b=c时取“=”.
∴${({{S_{△ABC}}})_{max}}=\frac{1}{2}bcsinA=\frac{1}{2}×4({2+\sqrt{3}})×\frac{1}{2}=2+\sqrt{3}$.
点评 本题考查三角函数知识的运用,考查余弦定理、基本不等式,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{7}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 丁酉年 | B. | 戊未年 | C. | 乙未年 | D. | 丁未年 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
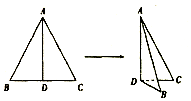 如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )
如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )| A. | $\frac{13}{2}π$ | B. | $\frac{13}{3}π$ | C. | $\frac{{13\sqrt{3}}}{2}π$ | D. | $\frac{{13\sqrt{3}}}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | (0,$\frac{5}{2}$] | C. | [$\frac{5}{2}$,4] | D. | [$\frac{5}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com