
·ЦОц ЈЁ1Ј©ЙиPЈЁx0Ј¬y0Ј©Ј¬AЈЁx1Ј¬y1Ј©Ј¬BЈЁ-x1Ј¬-y1Ј©Ј¬ҙъИлНЦФІ·ҪіМөГ$\frac{{{y}_{0}}^{2}-{{y}_{1}}^{2}}{{{x}_{0}}^{2}-{{x}_{1}}^{2}}=-\frac{{b}^{2}}{{a}^{2}}$Ј¬УЙЦұПЯPAЎўPBөДРұВКЦ®»эОӘ-$\frac{1}{4}$Ј¬өГөҪ$\frac{{b}^{2}}{{{a}^{2}}_{\;}}$=$\frac{1}{4}$Ј¬УЙҙЛДЬЗуіцНЦФІCөДАлРДВКЈ®
ЈЁ2Ј©УЙe=$\frac{c}{a}=\frac{\sqrt{3}}{2}$Ј¬өГ$\frac{b}{a}=\frac{1}{2}$Ј¬ҙУ¶ш$\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1Ј¬c=$\sqrt{3}b$Ј¬Ҫ№өгF1ЈЁ-$\sqrt{3}b$Ј¬0Ј©Ј¬ЙиMNЈәy=kЈЁx-$\sqrt{3}b$Ј©Ј¬БӘБў$\left\{\begin{array}{l}{y=kЈЁx-\sqrt{3}bЈ©}\\{{x}^{2}+4{y}^{2}=4{b}^{2}}\end{array}\right.$Ј¬өГ$ЈЁ4{k}^{2}+1Ј©{x}^{2}-8\sqrt{3}{k}^{2}bx+12{k}^{2}{b}^{2}-4{b}^{2}=0$Ј¬УЙҙЛАыУГОӨҙп¶ЁАнЎўПтБҝөДКэБҝ»эЈ¬ҪбәПТСЦӘМхјюДЬЗуіцkөДИЎЦө·¶О§Ј®
Ҫвҙр ҪвЈәЈЁ1Ј©ЙиPЈЁx0Ј¬y0Ј©Ј¬AЈЁx1Ј¬y1Ј©Ј¬BЈЁ-x1Ј¬-y1Ј©Ј¬
Фт$\left\{\begin{array}{l}{\frac{{{x}_{0}}^{2}}{{a}^{2}}+\frac{{{y}_{0}}^{2}}{{b}^{2}}=1}\\{\frac{{{x}_{1}}^{2}}{{a}^{2}}+\frac{{{y}_{1}}^{2}}{{b}^{2}}=1}\end{array}\right.$Ј¬Ўа$\frac{{{y}_{0}}^{2}-{{y}_{1}}^{2}}{{{x}_{0}}^{2}-{{x}_{1}}^{2}}=-\frac{{b}^{2}}{{a}^{2}}$Ј¬
ЎЯ${k}_{PA}•{k}_{PB}=\frac{{y}_{0}-{y}_{1}}{{x}_{0}-{x}_{1}}$•$\frac{{y}_{0}+{y}_{1}}{{x}_{0}+{x}_{1}}$=$\frac{{{y}_{0}}^{2}-{{y}_{1}}^{2}}{{{x}_{0}}^{2}-{{x}_{1}}^{2}}=-\frac{1}{4}$Ј¬
Ўа$\frac{{b}^{2}}{{{a}^{2}}_{\;}}$=$\frac{1}{4}$Ј¬
ЎаНЦФІCөДАлРДВКe=$\sqrt{1-\frac{{b}^{2}}{a2}}$=$\sqrt{1-\frac{1}{4}}=\frac{\sqrt{3}}{2}$Ј®
ЈЁ2Ј©ЎЯe=$\frac{c}{a}=\frac{\sqrt{3}}{2}$Ј¬Ўа$\frac{b}{a}=\frac{1}{2}$Ј¬
Ўа$\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1Ј¬c=$\sqrt{3}b$Ј¬Ҫ№өгF1ЈЁ-$\sqrt{3}b$Ј¬0Ј©Ј¬
ЙиMNЈәy=kЈЁx-$\sqrt{3}b$Ј©Ј¬
БӘБў$\left\{\begin{array}{l}{y=kЈЁx-\sqrt{3}bЈ©}\\{{x}^{2}+4{y}^{2}=4{b}^{2}}\end{array}\right.$Ј¬өГ$ЈЁ4{k}^{2}+1Ј©{x}^{2}-8\sqrt{3}{k}^{2}bx+12{k}^{2}{b}^{2}-4{b}^{2}=0$Ј¬
ЙиMЈЁx1Ј¬y1Ј©Ј¬NЈЁx2Ј¬y2Ј©Ј¬Фт${x}_{1}+{x}_{2}=\frac{8\sqrt{3}{k}^{2}b}{4{k}^{2}+1}$Ј¬${x}_{1}{x}_{2}=\frac{12{k}^{2}{b}^{2}-4{b}^{2}}{4{k}^{2}+1}$Ј¬
${y}_{1}{y}_{2}={k}^{2}ЈЁ{x}_{1}-\sqrt{3}bЈ©ЈЁ{x}_{2}-\sqrt{3}bЈ©$=${k}^{2}[{x}_{1}{x}_{2}-\sqrt{3}bЈЁ{x}_{1}+{x}_{2}Ј©+3{b}^{2}]$Ј¬
Ўа$\overrightarrow{{F}_{1}M}•\overrightarrow{{F}_{1}N}$Јј0Ј¬
ЎаЈЁx1+$\sqrt{3}b$Ј¬y1Ј©•ЈЁ${x}_{2}+\sqrt{3}b$Ј¬y2Ј©=ЈЁ${x}_{1}+\sqrt{3}b{x}_{1}{x}_{2}+\sqrt{3}b$Ј©+y1y2
=${x}_{1}{x}_{2}+\sqrt{3}bЈЁ{x}_{1}+{x}_{2}Ј©+3{b}^{2}$+${k}^{2}[{x}_{1}{x}_{2}-\sqrt{3}bЈЁ{x}_{1}+{x}_{2}Ј©+3{b}^{2}]$
=ЈЁ1+k2Ј©x1x2-$\sqrt{3}b$ЈЁx1+x2Ј©ЈЁ1-k2Ј©+3b2ЈЁ1+k2Ј©
=$\frac{ЈЁ1+{k}^{2}Ј©ЈЁ12{k}^{2}{b}^{2}-4{b}^{2}Ј©}{4{k}^{2}+1}$+$\frac{24{k}^{2}{b}^{2}ЈЁ1-{k}^{2}Ј©}{4{k}^{2}+1}$+$\frac{-3{b}^{2}ЈЁ1+{k}^{2}Ј©ЈЁ4{k}^{2}+1Ј©}{4{k}^{2}+1}$Јј0Ј¬
ЎаЈЁ1+k2Ј©ЈЁ12k2-4Ј©+24k2ЈЁ1-k2Ј©+3ЈЁ1+k2Ј©ЈЁ4k2+1Ј©Јј0Ј¬
ХыАнЈ¬өГ${k}^{2}Јј\frac{1}{47}$Ј¬ҪвөГkөДИЎЦө·¶О§КЗЈЁ-$\frac{\sqrt{47}}{47}Ј¬\frac{\sqrt{47}}{47}$Ј©Ј®
өгЖА ұҫМвҝјІйНЦФІөДАлРДВКөДЗу·ЁЈ¬ҝјІйКөКэөДИЎЦө·¶О§Зу·ЁЈ¬КЗЦРөөМвЈ¬ҪвМвКұТӘИПХжЙуМвЈ¬ЧўТвОӨҙп¶ЁАнЎўНЦФІРФЦКөДәПАнФЛУГЈ®


 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
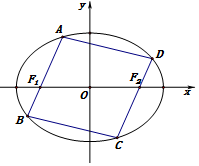
 ИзНјЈ¬ТСЦӘНЦФІCЈә$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1ЈЁaЈҫbЈҫ0Ј©$УлЛ«ЗъПЯ$\frac{x^2}{4}-\frac{y^2}{2}=1$УРПаН¬өДҪ№өгЈ¬ЗТНЦФІC№эөгPЈЁ2Ј¬1Ј©Ј¬ИфЦұПЯlУлЦұПЯOPЖҪРРЗТУлНЦФІCПаҪ»УЪөгAЈ¬BЈ®
ИзНјЈ¬ТСЦӘНЦФІCЈә$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1ЈЁaЈҫbЈҫ0Ј©$УлЛ«ЗъПЯ$\frac{x^2}{4}-\frac{y^2}{2}=1$УРПаН¬өДҪ№өгЈ¬ЗТНЦФІC№эөгPЈЁ2Ј¬1Ј©Ј¬ИфЦұПЯlУлЦұПЯOPЖҪРРЗТУлНЦФІCПаҪ»УЪөгAЈ¬BЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | y=lnx3 | BЈ® | y=-x2 | CЈ® | y=-$\frac{1}{x}$ | DЈ® | y=x|x| |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ТСЦӘНЦФІEөДЦРРДФЪФӯөгЈ¬Ҫ№өгF1ЎўF2ФЪxЦбЙПЈ¬АлРДВКОӘ$\frac{1}{2}$Ј¬ФЪНЦФІEЙПУРТ»¶ҜөгAУлF1ЎўF2өДҫаАлЦ®әНОӘ4Ј¬
ТСЦӘНЦФІEөДЦРРДФЪФӯөгЈ¬Ҫ№өгF1ЎўF2ФЪxЦбЙПЈ¬АлРДВКОӘ$\frac{1}{2}$Ј¬ФЪНЦФІEЙПУРТ»¶ҜөгAУлF1ЎўF2өДҫаАлЦ®әНОӘ4Ј¬Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
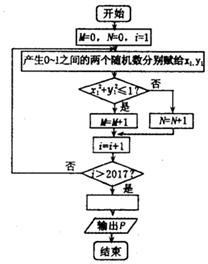 ИзНјЛщКҫЈ¬К№УГДЈДв·Ҫ·Ё№АјЖФІЦЬВКЦөөДіМРтҝтИтЈ¬PұнКҫ№АјЖөДҪб№ыЈ¬ёХНјЦРҝХ°ЧҝтДЪУҰМоИлP=ЈЁЎЎЎЎЈ©
ИзНјЛщКҫЈ¬К№УГДЈДв·Ҫ·Ё№АјЖФІЦЬВКЦөөДіМРтҝтИтЈ¬PұнКҫ№АјЖөДҪб№ыЈ¬ёХНјЦРҝХ°ЧҝтДЪУҰМоИлP=ЈЁЎЎЎЎЈ©| AЈ® | $\frac{M}{2017}$ | BЈ® | $\frac{2017}{M}$ | CЈ® | $\frac{4M}{2017}$ | DЈ® | $\frac{2017}{4M}$ |
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com