Question

2．在正方体ABCD-A₁B₁C₁D₁中，EF分别是棱AA₁，A₁C₁的中点，求：
（1）CE与平面ABCD所成角的余弦值；
（2）EF与平面ABCD所成角的大小．

Answer 1

分析 （1）首先根据已知条件，指出线面的夹角，进一步利用解直角三角形知识求出结果．
（2）指出线面的夹角，进一步利用解直角三角形知识求出结果．

解答 解：（1）在正方体ABCD-A₁B₁C₁D₁中，设棱长为2，
E、F分别是棱AA₁，A₁D₁的中点，连接AC，
由于：AE⊥平面ABCD，
所以：∠ECA就是直线CE与平面ABCD所成角，
则：$AC=2\sqrt{2}$，AE=1
利用勾股定理解得：$CE=\sqrt{{AC}^{2}+{AE}^{2}}$=3
所以：cos∠ECA=$\frac{AC}{CE}=\frac{2\sqrt{2}}{3}$
（2）E、F分别是棱AA₁，A₁D₁的中点，
所以：△A₁EF为等腰三角形．
EF与平面ABCD所成角，即EF与平面A₁B₁C₁D₁所成的角．
EA⊥平面ABCD，
平面ABCD∥平面A₁B₁C₁D₁
所以：∠EFA₁就是EF与平面ABCD所成角．
由于△A₁EF为等腰三角形，
所以：∠EFA₁=45°
即：EF与平面ABCD所成角的大小为45°．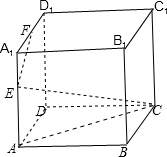

点评 本题考查的知识要点：线面的夹角问题，解直角三角形知识的应用．