
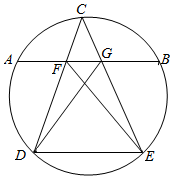
分析 连接AD,DE,EB,由A,D,E,B四点共圆,可得对角互补,点C是弧AB的中点,可得等弧所对圆周角相等,即可得到四边形DFEG的对角互补,可得四点D、F、G、E共圆,在EF上取一点K,运用相似三角形的判定可得△FDK∽△GDE,△FDG∽△KDE,再由对应边成比例,即可得到结论.
解答 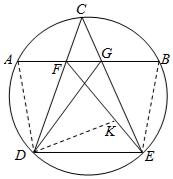 证明:连接AD,DE,EB,
证明:连接AD,DE,EB,
由A,D,E,B四点共圆,得∠ADE+∠B=180°,
∵∠ADE=∠ADC+∠CDE,
∴∠ADC+∠CDE+∠B=180°①
∵点C是弧AB的中点,
∴∠ADC=∠BEC ②
由①②,得∴∠BEC+∠CDE+∠B=180°,
即(∠BEC+∠B)+∠CDE=180°,
∴∠EGA+∠CDE=180°,
则四边形DFEG内接于圆,
即有∠DFE=DGE,∠FGD=∠FED,
在EF上取一点K,使得∠FDK=∠EDG,
∠FDK+∠EDK=∠FDE=∠FDG+∠EDG,
可得∠EDK=∠FDG,
则△FDK∽△GDE,△FDG∽△KDE,
即有$\frac{FK}{FD}$=$\frac{GE}{GD}$,$\frac{EK}{DE}$=$\frac{FG}{DG}$,
即FK•DG=DF•GE,EK•DG=DE•FG,
相加可得,(FK+EK)•DG=DF•GE+DE•FG.
则DG•EF=FD•GE+DE•FG.
点评 本题考查与圆有关的比例线段,解本题的关键是由所证的结论观察出其成立的等价条件:四点D、F、G、E共圆,考查相似三角形的判定和性质,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 20° | B. | 70° | C. | 110° | D. | 160° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
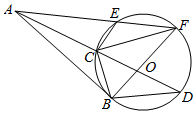 如图,AB是圆O的一条切线,切点为B,AF、AD都是圆O的割线,AD交圆O于点C,AF交圆O于点E,且∠ABC=∠ECF,连接EC、FB,BF过圆心O.
如图,AB是圆O的一条切线,切点为B,AF、AD都是圆O的割线,AD交圆O于点C,AF交圆O于点E,且∠ABC=∠ECF,连接EC、FB,BF过圆心O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com