
分析 分析已知条件中:sin230°+sin290°+sin2150°=$\frac{3}{2}$,sin210°+sin2670°+sin2130°=$\frac{3}{2}$.可以发现等式左边参加累加的三个均为正弦的平方,且三个角组成一个以60°为公差的等差数列,右边是常数,由此不难得到结论.
解答 解:一般性的命题为${sin^2}(α-{60°})+{sin^2}α+{sin^2}(α+{60°})=\frac{3}{2}$.
证明:左边=$\frac{1-cos(2α-120°)}{2}$+$\frac{1-cos2α}{2}$+$\frac{1-cps(2α+120°)}{2}$
=$\frac{3}{2}$-[cos(2α-120°)+cos2α+cos(2α+120°)]=$\frac{3}{2}$.
点评 本题考查归纳推理,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想),(3)论证.


科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,$\root{3}{12}$) | C. | (1,$\root{3}{4}$) | D. | (2,$\root{3}{10}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
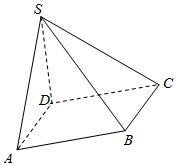 如图,在四棱锥S-ABCD中,底面ABCD为梯形,AD∥BC,AD⊥平面SCD,AD=DC=BC=1,SD=2,∠SDC=120°.
如图,在四棱锥S-ABCD中,底面ABCD为梯形,AD∥BC,AD⊥平面SCD,AD=DC=BC=1,SD=2,∠SDC=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln2 | B. | 2 | C. | 2+$\frac{1}{2}$ln2 | D. | 2+ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com