
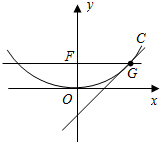
 设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).
设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).分析 (1)求出G点的坐标为(p,$\frac{p}{2}$),推出切线的斜率,得到过点G的切线方程,然后求出p,即可求出抛物线的方程.
(2)设切点Q(x0,$\frac{{x}_{0}^{2}}{4}$)抛物线在Q点处的切线斜率为$\frac{{x}_{0}}{2}$,求出切线方程,点(0,-2)在切线上,求解Q,然后得到所求切线方程.
解答 解:(1)由x2=2px得y=$\frac{1}{2p}$x2,
当y=$\frac{p}{2}$得x=±p,∴G点的坐标为(p,$\frac{p}{2}$),…(2分)
y′=$\frac{1}{p}x$,y′|x=p=1,
过点G的切线方程为y-$\frac{p}{2}$=x-p即y=x-$\frac{p}{2}$,…(5分)
令x=0得y=-$\frac{p}{2}$,
∴$-\frac{p}{2}=-1$即p=2,即抛物线的方程为x2=4x…(7分)
(2)设切点Q(x0,$\frac{{x}_{0}^{2}}{4}$).(x0<0),由y′=$\frac{x}{2}$,知抛物线在Q点处的切线斜率为$\frac{{x}_{0}}{2}$,…(9分)
∴所求切线方程y-$\frac{{x}_{0}^{2}}{4}$=$\frac{{x}_{0}}{2}$(x-x0),
即y=$\frac{{x}_{0}}{2}x-\frac{{x}_{0}^{2}}{4}$.…(11分)
∵点(0,-2)在切线上,
∴-2=-$\frac{{x}_{0}^{2}}{4}$,
∴x0=2$\sqrt{2}$(舍去)或x0=-2$\sqrt{2}$. …(13分)
∴所求切线方程为y=-$\sqrt{2}x-2$. …(14分)
点评 本题考查直线与抛物线方程的综合应用,曲线的切线方程的求法,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:解答题
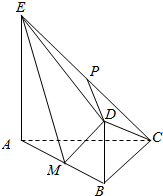 如图,平面ABDE⊥平面ABC,AC⊥BC,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,AE=2BD=4,P、M分别为CE,AB的中点.
如图,平面ABDE⊥平面ABC,AC⊥BC,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,AE=2BD=4,P、M分别为CE,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,-2) | B. | (-2,2) | C. | (-1,2) | D. | (2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2011年3月11日,日本发生了9.0级大地震,同时导致了福岛核电站的泄露事件,给环境带来的一定的污染,也给世界各国的人们对环境的保护敲响了警钟.根据空气质量指数API(为整数)的不同,可将空气质量分级如表:
2011年3月11日,日本发生了9.0级大地震,同时导致了福岛核电站的泄露事件,给环境带来的一定的污染,也给世界各国的人们对环境的保护敲响了警钟.根据空气质量指数API(为整数)的不同,可将空气质量分级如表:| API | 0~50 | 51~200 | 101~150 | 151~200 | 201~250 | 251~300 | >300 |
| 级别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 状况 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com