
 2011年3月11日,日本发生了9.0级大地震,同时导致了福岛核电站的泄露事件,给环境带来的一定的污染,也给世界各国的人们对环境的保护敲响了警钟.根据空气质量指数API(为整数)的不同,可将空气质量分级如表:
2011年3月11日,日本发生了9.0级大地震,同时导致了福岛核电站的泄露事件,给环境带来的一定的污染,也给世界各国的人们对环境的保护敲响了警钟.根据空气质量指数API(为整数)的不同,可将空气质量分级如表:| API | 0~50 | 51~200 | 101~150 | 151~200 | 201~250 | 251~300 | >300 |
| 级别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 状况 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
分析 (1)根据频率分布直方图,利用频率和为1,求出x的值;
(2)根据空气质量为良与轻微污染的频率和,求出对应的频数即可;
(3)求出该城市一年中每天空气质量为良或轻微污染的频率,利用对立事件得出所求的概率.
解答 解:(1)根据频率分布直方图,得;
50x=1-($\frac{3}{1825}$+$\frac{2}{365}$+$\frac{7}{1825}$+$\frac{3}{1825}$+$\frac{8}{9125}$)×50
=1-$\frac{123}{9125}$×50
=$\frac{5950}{1825}$,
解得x=$\frac{119}{1825}$;
(2)空气质量为良与轻微污染的频率和为
$\frac{119}{18250}$×50+$\frac{2}{365}$×50=$\frac{219}{365}$,
∴一年中空气质量为良和轻微污染的总天数为
365×$\frac{219}{365}$=219;
(3)该城市一年中每天空气质量为良或轻微污染的概率为
$\frac{119}{18250}$×50+$\frac{2}{365}$×50=$\frac{219}{365}$=$\frac{3}{5}$;
则空气质量不为良且不为轻微污染的概率为
1-$\frac{3}{5}$=$\frac{2}{5}$.
点评 本题考查了频率分布直方图的应用问题,也考查了用频率估计随机事件的概率的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
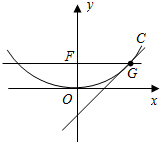 设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).
设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com