
分析 根据递减的等比数列特征求出a1、a2、a3的值,即可求出公比,利用等比数列的前n项和公式求出式子的值.
解答 解:由题意可得,a1=4,a2=2,a3=1,
所以公比q=$\frac{1}{2}$,
则$\frac{{S}_{8}}{1-{q}^{4}}$=$\frac{\frac{4(1-{q}^{8})}{1-q}}{1-{q}^{4}}$=$\frac{4(1+{q}^{4})}{1-q}$=4(1+$\frac{1}{16}$)×2=$\frac{17}{2}$,
故答案为:$\frac{17}{2}$.
点评 本题考查递减等比数列的性质,以及等比数列的前n项和公式,属于中档题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题是p∨q假命题 | B. | 命题是p∧q真命题 | ||
| C. | 命题是(?p)∨(?q)真命题 | D. | 命题是(?p)∧(?q)真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{8}$个单位长度 | B. | 向右平移$\frac{π}{8}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
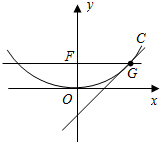 设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).
设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
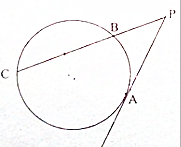 如图,PA是圆的切线,A为切点,PBC是圆的割线,且PB=$\frac{1}{2}$BC,则$\frac{PA}{PB}$=$\sqrt{3}$.
如图,PA是圆的切线,A为切点,PBC是圆的割线,且PB=$\frac{1}{2}$BC,则$\frac{PA}{PB}$=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
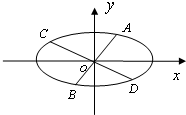 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com