
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点;
是否过定点;
(3)若![]() 为圆
为圆![]() 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为 ,求四边形
,求四边形![]() 的面积的最大值.
的面积的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一个长方体的平面展开图及该长方体的直观图的示意图如图所示.
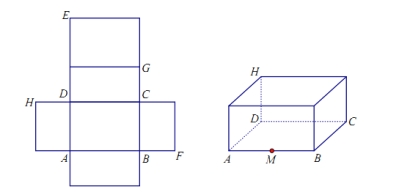
(1)请将字母![]() 标记在长方体相应的顶点处(不需说明理由);
标记在长方体相应的顶点处(不需说明理由);
(2)在长方体中,判断直线![]() 与平面
与平面![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)在长方体中,设![]() 的中点为
的中点为![]() ,且
,且![]() ,
,![]() ,求证:
,求证:
![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时.若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数x与骑兵个数y表示每天的利润W(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,四边形
,四边形![]() 为正方形,点
为正方形,点![]() 分别为线段
分别为线段![]() 上的点,
上的点,![]() .
.
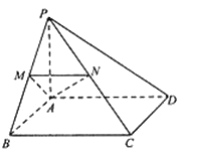
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:当点![]() 不与点
不与点![]() 重合时,
重合时,![]() 平面
平面![]() ;
;
(3)当![]() 时,求点
时,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料 ![]() ,五合板
,五合板 ![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料 ![]() ,五合板
,五合板 ![]() ,生产每个书橱需要方木料
,生产每个书橱需要方木料 ![]() ,五合板
,五合板 ![]() ,出售一张书桌可获利润
,出售一张书桌可获利润 ![]() 元,出售一个书橱可获利润
元,出售一个书橱可获利润 ![]() 元.
元.
(1)如果只安排生产书桌,可获利润多少?
(2)如果只安排生产书橱,可获利润多少?
(3)怎祥安排生产可使所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在数列{an}中,Sn为其前n项和,若an>0,且4Sn=an2+2an+1(n∈N*),数列{bn}为等比数列,公比q>1,b1=a1,且2b2,b4,3b3成等差数列.
(1)求{an}与{bn}的通项公式;
(2)令cn=![]() ,若{cn}的前项和为Tn,求证:Tn<6.
,若{cn}的前项和为Tn,求证:Tn<6.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)记![]() ,求证:函数
,求证:函数![]() 在区间
在区间![]() 内有且仅有一个零点;
内有且仅有一个零点;
(2)用![]() 表示
表示![]() 中的最小值,设函数
中的最小值,设函数![]() ,若关于
,若关于![]() 的方程
的方程![]() (其中
(其中![]() 为常数)在区间
为常数)在区间![]() 有两个不相等的实根
有两个不相等的实根![]() ,记
,记![]() 在
在![]() 内的零点为
内的零点为![]() ,试证明:
,试证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() :
: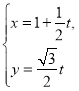 (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com