
| A. | 240 | B. | 180 | C. | 150 | D. | 540 |
分析 每所大学至少保送一人,可以分类来解,当5名学生分成2,2,1时,共有$\frac{1}{2}$C52C32A33,当5名学生分成3,1,1时,共有$\frac{1}{2}$C53${C}_{2}^{1}$A33,根据分类计数原理得到结果.
解答 解:当5名学生分成2,2,1或3,1,1两种形式,
当5名学生分成2,2,1时,共有$\frac{1}{2}$C52C32A33=90种结果,
当5名学生分成3,1,1时,共有$\frac{1}{2}$C53${C}_{2}^{1}$A33=60种结果,
∴根据分类计数原理知共有90+60=150种,
故选:C.
点评 本题考查了分组分配问题,关键是如何分组,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}+\sqrt{3}}}{2}$ | B. | $\sqrt{6}+\sqrt{3}$ | C. | $\frac{{\sqrt{5+2\sqrt{2}}}}{2}$ | D. | $\sqrt{5+2\sqrt{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
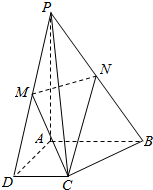 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com