
| A. | 1 | B. | $\sqrt{5}$ | C. | $\sqrt{7}$ | D. | 3 |
分析 利用向量垂直与数量积的关系可得xy=2,再利用向量模的计算公式通过二次函数的最值即可得出结果.
解答 解:∵平面向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(2,y),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\overrightarrow{a}•\overrightarrow{b}$=0,即有2+xy=0,即xy=-2,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{9+(x+y)^{2}}$=$\sqrt{9+(y-\frac{2}{y})^{2}}$≥3,
当且仅当x=-$\sqrt{2}$,y=$\sqrt{2}$取等号.
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|的最小值为3.
故选:D.
点评 本题考查了向量垂直与数量积的关系、向量模的计算公式,属于基础题.


科目:高中数学 来源: 题型:填空题
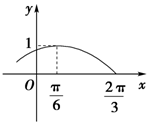 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
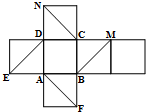 如图是正方体平面展开图,在这个正方体中
如图是正方体平面展开图,在这个正方体中| A. | ①②③ | B. | ②④ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com