
分析 (1)$\overrightarrow{m}$$•\overrightarrow{n}$=bsinA,利用数量积运算及其正弦定理、余弦定理即可得出,
(2)由余弦定理32=a2+c2-ac,再利用基本不等式的性质即可得出.
解答 解:(1)$\overrightarrow{m}$$•\overrightarrow{n}$=asinA+(sinB+sinC)(b-c)=bsinA,
即:由正弦定理可知,$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$,
a2+(b+c)(b-c)=ba,
整理得:c2=a2+b2-ab,
由余弦定理得:c2=a2+b2-2abcosC,
cosC=$\frac{1}{2}$,
C=$\frac{π}{3}$;
(2)3=c2=a2+b2-ab≥2ab-ab=ab,
∴ab≤3,
a+2b≤2$\sqrt{a•2b}$=2$\sqrt{6}$,
当且仅当a=2b=$\sqrt{6}$,
故a+2b的最大值2$\sqrt{6}$.
点评 本题考查了正弦定理与余弦定理的应用、基本不等式的性质、向量数量积运算性质,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
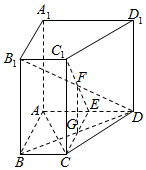 如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.
如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |z1|+|z2|>|z1+z2| | B. | |z1|-|z2|>|z1-z2| | C. | |z1|+|z2|≥|z1+z2| | D. | |z1|-|z2|≥|z1-z2| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com