
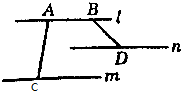
分析 假设AC与BD共面,则A、B、C、D四点共面,从而推导出直线l,m,n共面,与已知直线l,m,n不共面相矛盾,由此能证明AC与BD是异面直线.
解答 证明:假设AC与BD共面,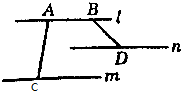
则A、B、C、D四点共面,
∵A,B,D三点不共线,∴A、B、D三点确定一个平面,设为α,
∵A、C、D三点不共线,∴A、C、D三点确定一个平面,设为β,
∵A、B、C、D四点共面,
∴α,β是同一个平面,
∵l∥n,∴直线l,n共面于平面α,
∵l∥m,∴直线l,m共面于平面β,
∴直线l,m,n共面,与已知直线l,m,n不共面相矛盾,
∴假设不成立,∴AC与BD是异面直线.
点评 本题考查两直线是异面直线的证明,是中档题,解题时要认真审题,注意空间基本定理及推论的合理运用.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
| 队员编号 | 1 | 2 | 3 | 4 | 5 |
| 甲班成绩 | 31 | 34 | 33 | 29 | 28 |
| 乙班成绩 | 27 | 31 | 30 | X | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
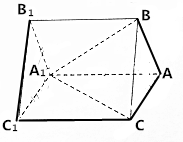 在三棱柱ABC-A1B1C1中已知AB=AC=AA1=2,∠BAA1=∠CAA1=60°,异面直线A1C1与BC成角为45°.
在三棱柱ABC-A1B1C1中已知AB=AC=AA1=2,∠BAA1=∠CAA1=60°,异面直线A1C1与BC成角为45°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在(0,+∞)上单调递增的奇函数 | B. | 在(0,+∞)上单调递减的奇函数 | ||
| C. | 在(0,+∞)上单调递增的偶函数 | D. | 在(0,+∞)上单调递减的偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
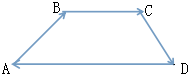 如图所示的四边形ABCD,已知$\overrightarrow{AB}$=(6,1),$\overrightarrow{BC}$=(x,y),$\overrightarrow{CD}$=(-2,-3)
如图所示的四边形ABCD,已知$\overrightarrow{AB}$=(6,1),$\overrightarrow{BC}$=(x,y),$\overrightarrow{CD}$=(-2,-3)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S5<S6 | B. | S5=S6 | C. | S7=S5 | D. | S7=S6. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com