
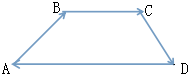
 如图所示的四边形ABCD,已知$\overrightarrow{AB}$=(6,1),$\overrightarrow{BC}$=(x,y),$\overrightarrow{CD}$=(-2,-3)
如图所示的四边形ABCD,已知$\overrightarrow{AB}$=(6,1),$\overrightarrow{BC}$=(x,y),$\overrightarrow{CD}$=(-2,-3)分析 (1)根据条件求得x(2-y)-y(-x-4)=0,即$f(x)=-\frac{1}{2}x$,结合-2≤x<1,可得y=f(x)的值域.
(2)根据$\overrightarrow{AC}•\overrightarrow{BD}$=0,∴求得(x+6)•(x-2)+(y+1)•(y-3)=0,?又$\overrightarrow{BC}∥\overrightarrow{DA}$,由(1)得x+2y=0,联立求得x、y的值,从而求得四边形ABCD的面积.
解答 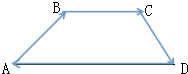 解:(1)∵$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=(x+4,y-2)$,
解:(1)∵$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=(x+4,y-2)$,
∴$\overrightarrow{DA}=(-x-4,2-y)$.
∵$\overrightarrow{BC}∥\overrightarrow{DA}且\overrightarrow{BC}=(x,y)$,∴x(2-y)-y(-x-4)=0,
∴$x+2y=0即y=-\frac{1}{2}x$,∴$f(x)=-\frac{1}{2}x$,
又∵-2≤x<1,∴y∈(-$\frac{1}{2}$,1],
即函数y=f(x)的值域为$(-\frac{1}{2},1]$;
(2)∵$\overrightarrow{BD}=\overrightarrow{BC}+\overrightarrow{CD}=(x-2,y-3),\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=(x+6,y+1)$,
由$\overrightarrow{AC}⊥\overrightarrow{BD}$,可得$\overrightarrow{AC}•\overrightarrow{BD}$=0,∴(x+6)•(x-2)+(y+1)•(y-3)=0,?
又$\overrightarrow{BC}∥\overrightarrow{DA}$,由(1)得x+2y=0?,联立可得:$\left\{{\begin{array}{l}{x=-6}\\{y=3}\end{array}}\right.或\left\{{\begin{array}{l}{x=2}\\{y=-1}\end{array}}\right.$.
若x=-6,y=3,则$\overrightarrow{AC}$=(0,4),$\overrightarrow{BD}$=(-8,0),∴S四边形ABCD=$\frac{1}{2}$|$\overrightarrow{AC}$|•|$\overrightarrow{BD}$|=16,
若x=2,y=-1,则$\overrightarrow{AC}$=(8,0),$\overrightarrow{BD}$=(0,-4),∴S四边形ABCD=$\frac{1}{2}$|$\overrightarrow{AC}$|•|$\overrightarrow{BD}$|=16,
综上:四边形ABCD的面积为16.
点评 本题主要考查两个向量的加减法及其几何意义,两个向量的数量积的运算,属于中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 53 | B. | 35 | C. | $A_5^3$ | D. | 5! |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com