
分析 (Ⅰ)求出函数的导数,根据f'(1)=3,求出a的值,根据f(1)=2求出b的值即可;
(Ⅱ)求出函数的导数,得到函数的单调区间,通过讨论a的范围,求出函数的最小值即可;
(Ⅲ)问题转化为f(x1)max<g(x2)max,结合函数的单调性求出a的范围即可.
解答 解:(Ⅰ)由f(x)=lnx-ax得$f'(x)=\frac{1}{x}-a=\frac{-ax+1}{x}$,
f'(1)=3⇒1-a=3⇒a=-2,
则f(x)=lnx+2x,f(1)=2点(1,2)为切点,
则2=3+b
⇒b=-1,
(Ⅱ)由f(x)=lnx-ax$f'(x)=\frac{1}{x}-a=\frac{-ax+1}{x}$,
∴f(x)在(0,$\frac{1}{a}$)递增,在($\frac{1}{a}$,+∞)递减,
①当$\frac{1}{a}$≤1,即a≥1时,函数f(x)在区间[1,2]上是减函数,
∴f(x)的最小值是f(2)=ln2-2a;
②当$\frac{1}{a}$≥2,即$0<a≤\frac{1}{2}$时,函数f(x)在区间[1,2]上是增函数,
∴f(x)的最小值是f(1)=-a;
③当1<$\frac{1}{a}$<2,即$\frac{1}{2}$<a<1时,函数f(x)在[1,$\frac{1}{a}$]上是增函数,在[$\frac{1}{a}$,2]是减函数.
又f(2)-f(1)=ln2-a,
∴当$\frac{1}{2}$<a<ln2时,最小值是f(1)=-a,
当ln2≤a<1时,最小值为f(2)=ln2-2a;
综上可知,当0<a<ln2时,函数f(x)的最小值是f(x)min=-a;
当a≥ln2时,函数f(x)的最小值是f(x)min=ln2-2a,
(Ⅲ)由条件得f(x1)max<g(x2)max,
又∵g(x2)max=2,
∴f(x1)max<2.
若a≤0,则f(x)在(0,+∞)上单调递增,
x→+∞,f(x)→+∞,不符题意;
∴a>0由Ⅱ可知$f(x{)_{max}}=f(\frac{1}{a})=-1-lna<2$,
得:$a>\frac{1}{e^3}$.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道综合题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨¬q为真 | B. | p∨q为真 | C. | ¬p∧¬q为真 | D. | p∧q为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
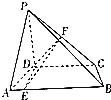 如图,四边形ABCD为等腰梯形,PD⊥平面ABCD,F为PC的中点,CD=AD=PD,AB=4AE=2CD.
如图,四边形ABCD为等腰梯形,PD⊥平面ABCD,F为PC的中点,CD=AD=PD,AB=4AE=2CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 26 | ||
| 合计 | 90 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com