
| A. | $({-∞,\frac{2}{5}}]$ | B. | $({-∞,\frac{1}{2}}]$ | C. | $({-∞,\frac{2}{3}}]$ | D. | (-∞,1] |
分析 由等比数列通项公式得${a}_{n}+(-1)^{n}$=2n,从而${a}_{n}={2}^{n}-(-1)^{n}$,再由等比数列前n项和公式得a1+a2+…+an=${2}^{n+1}-\frac{3}{2}-\frac{1}{2}×(-1)^{n}$,由此得到对于任意的n∈N*,不等式a1+a2+…+an≥λan+1恒成立,等价于对于任意的n∈N*,不等式λ≤$\frac{{2}^{n+1}-\frac{3}{2}-\frac{1}{2}×(-1)^{n}}{{2}^{n+1}-(-1)^{n+1}}$恒成立,由此能求出实数λ的取值范围.
解答 解:∵在数列{an}中,已知a1=3,且数列$\left\{{{a_n}+{{({-1})}^n}}\right\}$是公比为2的等比数列,
∴${a}_{n}+(-1)^{n}$=2n,
∴${a}_{n}={2}^{n}-(-1)^{n}$,
∴a1+a2+…+an=$\frac{2(1-{2}^{n})}{1-2}$-$\frac{-1×[1-(-1)^{n}]}{1-(-1)}$=${2}^{n+1}-\frac{3}{2}-\frac{1}{2}×(-1)^{n}$,
∵对于任意的n∈N*,不等式a1+a2+…+an≥λan+1恒成立,
∴对于任意的n∈N*,不等式${2}^{n+1}-\frac{3}{2}-\frac{1}{2}×(-1)^{n}$≥λ[2n+1-(-1)n+1]恒成立,
∴对于任意的n∈N*,不等式λ≤$\frac{{2}^{n+1}-\frac{3}{2}-\frac{1}{2}×(-1)^{n}}{{2}^{n+1}-(-1)^{n+1}}$恒成立,
当n=1时,$\frac{{2}^{n+1}-\frac{3}{2}-\frac{1}{2}×(-1)^{n}}{{2}^{n+1}-(-1)^{n+1}}$取最大值$\frac{2}{3}$,
∴$λ≤\frac{2}{3}$.
∴实数λ的取值范围是(-∞,$\frac{2}{3}$].
故选:C.
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意等比数列的性质、等价转化思想的合理运用.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
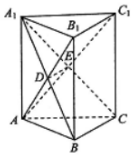 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在△ABC中,AB=BC=$\sqrt{6}$,∠ABC=90°,点D为AC的中点,将△ABD沿BD折起到△PBD的位置,使PC=PD,连接PC,得到三棱锥P-BCD,若该三棱锥的所有顶点都在同一球面上,则该球的表面积是( )
如图,在△ABC中,AB=BC=$\sqrt{6}$,∠ABC=90°,点D为AC的中点,将△ABD沿BD折起到△PBD的位置,使PC=PD,连接PC,得到三棱锥P-BCD,若该三棱锥的所有顶点都在同一球面上,则该球的表面积是( )| A. | π | B. | 3π | C. | 5π | D. | 7π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(π)<g(3)<g($\sqrt{2}$) | B. | g(π)<g($\sqrt{2}$)<g(3) | C. | g($\sqrt{2}$)<g(3)<g(π) | D. | g($\sqrt{2}$)<g(π)<g(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6051 | B. | 4034 | C. | 2017 | D. | 1009 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com