
分析 由已知可知排列规律是(m,n)(m,n∈N*),且m+n的和从2开始,依次是3,4…增大,其中m也是依次增大,按规律分组:第一组(1,1);第二组(1,2),(2,1);第三组(1,3),(2,2),(3,1);…求前10组有序实数对个数,第50项应在第10组中的第五个,分析“整数对”的分布规律,然后归纳推断出第50个数对.
解答 解:由已知可知:“整数对”(m,n)(m,n∈N*),m+n的值从2开始,依次是3,4…增大,其中m也是依次增大,
而m+n=2只有一个(1,1);
m+n=3有两个(1,2),(2,1);
m+n=4有3个(1,3),(2,2),(3,1);
…
m+n=11有10个(1,10),(2,9),…,(10,1);
其上面共有1+2+…+10=$\frac{11(1+10)}{2}$=55个;
所以第50个“整数对”是(5,6),
故答案为:(5,6).
点评 本题考查的知识点是归纳推理,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想),属于基础题.


科目:高中数学 来源: 题型:填空题
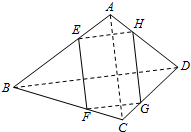 如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的点,并且AC∥面EFGH,BD∥面EFGH,AC=2,BD=4,当EFGH是菱形时,$\frac{AE}{EB}$的值是$\frac{AE}{EB}$.
如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的点,并且AC∥面EFGH,BD∥面EFGH,AC=2,BD=4,当EFGH是菱形时,$\frac{AE}{EB}$的值是$\frac{AE}{EB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {an}是公比为2的等比数列 | B. | {an}是公比为3的等比数列 | ||
| C. | {an}是公差为2的等差数列 | D. | {an}是公差为3的等差数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 4 | 2 | 3 | 5 |
| y | 38 | 20 | 31 | 51 |
| A. | 50 | B. | 60 | C. | 63 | D. | 59 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 分组 (日销售量) | 频率 (甲种酸奶) |
| [0,10] | 0.10 |
| (10,20] | 0.20 |
| (20,30] | 0.30 |
| (30,40] | 0.25 |
| (40,50] | 0.15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+(y-1)2=1 | B. | x2+(y+1)2=1 | C. | (x-1)2+y2=1 | D. | (x+1)2+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com