
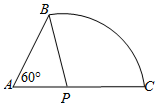
 某柱体实心铜制零件的截面边长是长度为55毫米线段AB和88毫米的线段AC以及圆心为P,半径为PB的一段圆弧BC构成,其中∠BAC=60°.
某柱体实心铜制零件的截面边长是长度为55毫米线段AB和88毫米的线段AC以及圆心为P,半径为PB的一段圆弧BC构成,其中∠BAC=60°.分析 (1)在△ABP中,由余弦定理建立方程,即可求半径PB的长度;
(2)求出V柱=S底•h,即可求该零件的重量.
解答 解:(1)∵AB=55,AC=88,BP=R,∠BAC=60°.AP=88-R,
∴在△ABP中,由余弦定理可得:BP2=AB2+AP2-2AB•AP•cos∠BAC,可得:R2=552+(88-R)2-2×55×(88-R)×cos60°,
∴解得:R=49mm.
(2)在△ABP中,AP=88-49=39mm,AB=55,BP=49,
cos∠BPA=$\frac{3{9}^{2}+4{9}^{2}-5{5}^{2}}{2×39×49}$=$\frac{897}{3822}$≈0.2347,
∴sin∠BPA≈0.972.
∴∠BPA=arcsin0.972.
V柱=S底•h=(S△ABP+S扇形BPC)•h=($\frac{1}{2}×55×39×\frac{\sqrt{3}}{2}$+$\frac{(arcsin0.972)π•4{9}^{2}}{360}$)•3
该零件的重量=($\frac{1}{2}×55×39×\frac{\sqrt{3}}{2}$+$\frac{(arcsin0.972)π•4{9}^{2}}{360}$)•3÷1000×8.9≈82.7.
点评 本题考查余弦定理的运用,考查面积的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 239 | B. | 240 | C. | 241 | D. | 242 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com