
分析 求出P的坐标,可得r,即可求出sinα,cosα,tanα.
解答 解:由$\left\{\begin{array}{l}{x-y=0}\\{2x+y-3=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$--------------------------------------------(3分)
∴P(1,1)--------------------------------------------------------------(4分)
∴r=$\sqrt{2}$,---------------------------------------------------------(6分)
∴sinα=cosα=$\frac{\sqrt{2}}{2}$,tanα=1.--------------------------------------(12分)
点评 本题考查三角函数的定义,考查两条直线的位置关系,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | 命题“?x0∈R,${x_0}^2-{x_0}≤0$”的否定为“?x∈R,x2-x>0” | |
| B. | 命题“在△ABC中,A>30°,则$sinA>\frac{1}{2}$”的逆否命题为真命题 | |
| C. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$,则$\overrightarrow a$与$\overrightarrow b$共线 | |
| D. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{2}{5}$ | C. | -$\frac{2}{5}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 横坐标伸长到原来的2倍,纵坐标不变 | |
| B. | 纵坐标伸长到原来的2倍,横坐标不变 | |
| C. | 横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变 | |
| D. | 纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
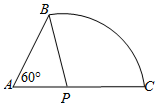 某柱体实心铜制零件的截面边长是长度为55毫米线段AB和88毫米的线段AC以及圆心为P,半径为PB的一段圆弧BC构成,其中∠BAC=60°.
某柱体实心铜制零件的截面边长是长度为55毫米线段AB和88毫米的线段AC以及圆心为P,半径为PB的一段圆弧BC构成,其中∠BAC=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com