
分析 延长BD至E,使得DE=BD,连接CE,△BCE中,由余弦定理建立方程,即可求边长BC的值.
解答 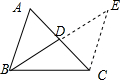 解:延长BD至E,使得DE=BD,连接CE,则cos∠BCE=-$\frac{\sqrt{6}}{6}$,CE=$\frac{4\sqrt{6}}{3}$,BE=2$\sqrt{5}$,
解:延长BD至E,使得DE=BD,连接CE,则cos∠BCE=-$\frac{\sqrt{6}}{6}$,CE=$\frac{4\sqrt{6}}{3}$,BE=2$\sqrt{5}$,
△BCE中,由余弦定理可得20=($\frac{4\sqrt{6}}{3}$)2+BC2-2×$\frac{4\sqrt{6}}{3}$×BC×(-$\frac{\sqrt{6}}{6}$),
∴BC2+$\frac{8}{3}$BC-$\frac{28}{3}$=0,
∴BC=2(负数舍去).
点评 本题考查余弦定理,考查学生的计算能力,比较基础.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
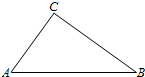 如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com