练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．观察这列数：1，2，3，3，2，1，2，3，4，4，3，2，3，4，5，5，4，3，4，5，6，6，5，4，…，则第2016个数是（　　）
    A．335B．336C．337D．338

    分析 观察这列数分布规律是：每6个数成一组，每组的第一个数（或最后一个数）依次为1，2，3，4，…，每组的数都是先按1递增两次，再相等一次，最后按1递减两次，且2016=336×6，得出第2016个数是336．

    解答 解：观察这列数分布为：1，2，3，3，2，1，2，3，4，4，3，2，3，4，5，5，4，3，4，5，6，6，5，4，…，
    发现每6个数成一组，每组的第一个数（或最后一个数）依次为1，2，3，4，…，
    每组的数都是先按1递增两次，再相等一次，
    最后按1递减两次：
    因为2016=336×6，
    所以第2016个数是336．
    故选：B．

    点评 本题考查了探究数列的项的规律性问题，解题的关键是观察数列的分布规律，从而求出对应的结论，是易错题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．已知实数1，m，4构成一个等比数列，则圆锥曲线$\frac{{x}^{2}}{m}$+y2=1的离心率为（　　）
    A．$\frac{\sqrt{2}}{2}$B．$\sqrt{3}$C．$\frac{\sqrt{2}}{2}$或$\sqrt{3}$D．$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{6}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设集合M={x|（x-3）（x+2）＜0}，N={x|x-1＞0}，则M∩N=（　　）
    A．（1，2）B．（1，3）C．（-1，2）D．（-1，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．计算：${C}_{n}^{0}×\frac{1}{2}$+$\frac{1}{2}$${C}_{n}^{1}$×（$\frac{1}{2}$）2+$\frac{1}{3}$${C}_{n}^{2}$×（$\frac{1}{2}$）3+…+$\frac{1}{n+1}$${C}_{n}^{n}$×（$\frac{1}{2}$）n+1=$\frac{1}{n+1}[（\frac{3}{2}）^{n+1}-1]$．．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知tanα=2，则sin2（$\frac{π}{2}$+α）-sin（3π+α）cos（2π-α）=$\frac{3}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设i为虚数单位，复数z=$\frac{3-i}{i}$，则z的共轭复数$\overline{z}$=（　　）
    A．-1-3iB．1-3iC．-1+3iD．1+3i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．若函数f（x）=ax2+20x+14（a＞0）对任意实数t，在闭区间[t-1，t+1]上总存在两实数x1、x2，使得|f（x1）-f（x2）|≥8成立，则实数a的取值范围是[8，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

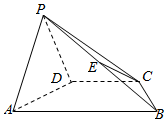    20．如图所示，四棱锥P-ABCD的底面是梯形，且AB∥CD，AB⊥平面PAD，E是PB中点，CD=PD=AD=$\frac{1}{2}$AB．
    （Ⅰ）求证：CE⊥AB；
    （Ⅱ）若CE=$\sqrt{3}$，AB=4，求三棱锥A-PCD的高．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．复数z满足z（2-i）=|1+2i|，则z的虚部为（　　）
    A．$\frac{{\sqrt{5}}}{5}$B．$\frac{{\sqrt{5}}}{5}i$C．1D．i

    查看答案和解析>>

    同步练习册答案