
分析 结合二次函数的图象可知,当且仅当区间[t-1,t+1]的中点是对称轴时,只要满足[t-1,t+1]上总存在两实数x1,x2,使得|f(x1)-f(x2)|≥8成立,则对其它任何情况必成立.
解答 解:因为a>0,所以二次函数f(x)=ax2+20x+14的图象开口向上.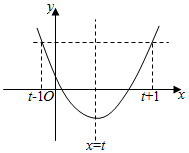
在闭区间[t-1,t+1]上总存在两实数x1,x2,使得|f(x1)-f(x2)|≥8成立,
只需t=-$\frac{10}{a}$时,f(t+1)-f(t)≥8,
即a(t+1)2+20(t+1)+14-(at2+20t+14)≥8,
即2at+a+20≥8,将t=-$\frac{10}{a}$代入得a≥8,
故答案为[8,+∞).
点评 本题考查了利用函数的最值研究恒成立问题的思路,同时结合函数图象分析问题是关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
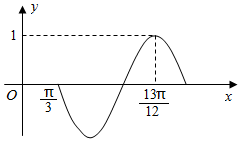 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
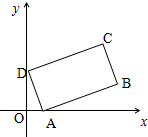 如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别位于x轴、y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}•\overrightarrow{OC}$的最大值是6.
如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别位于x轴、y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}•\overrightarrow{OC}$的最大值是6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com