
分析 根据题意求出原函数,然后根据积分运算法则,计算即可
解答 解:由于${∫}_{0}^{\frac{1}{2}}$$\frac{1+x}{\sqrt{1-{x}^{2}}}$dx
=${∫}_{0}^{\frac{1}{2}}$$\frac{1}{\sqrt{1-{x}^{2}}}$dx+${∫}_{0}^{\frac{1}{2}}$$\frac{x}{\sqrt{1-{x}^{2}}}$dx
=arcsinx${|}_{0}^{\frac{1}{2}}$+(-$\frac{1}{2}$$\sqrt{1-{x}^{2}}$)${|}_{0}^{\frac{1}{2}}$
=arcsin$\frac{1}{2}$-$\frac{\sqrt{3}}{4}$+$\frac{1}{2}$
则${∫}_{0}^{\frac{1}{2}}$$\frac{1+x}{\sqrt{1-{x}^{2}}}$dx=arcsin$\frac{1}{2}$-$\frac{\sqrt{3}}{4}$+$\frac{1}{2}$.
点评 本题主要考查定积分的计算,解题的关键是找到被积函数的原函数,此题是一道基础题


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
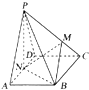 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=0.
如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com