
分析 (1)由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,能求出圆C在直角坐标系中的标准方程.
(2)求出点A的直角坐标为($\sqrt{3}$,0),圆心C($\sqrt{3}$,-1)是线段AB的中点,点B的直角坐标为($\sqrt{3}$,-2),由圆C的参数方程设点P($\sqrt{3}+2cosθ$,-1+2sinθ),则|PA|+|PB|=$\sqrt{(2cosθ)^{2}+(2sinθ-1)^{2}}$+$\sqrt{(2cosθ)^{2}+(2sinθ+1)^{2}}$=$\sqrt{10+2\sqrt{25-16si{n}^{2}θ}}$,由此能求出|PA|+|PB|的最大值.
解答 解:(1)∵圆C的极坐标方程为ρ=2$\sqrt{3}$cosθ-2sinθ,
∴圆C的极坐标方程为ρ2=2$\sqrt{3}$ρcosθ-2ρsinθ,
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
得${x}^{2}+{y}^{2}-2\sqrt{3}x+2y=0$,
∴圆C在直角坐标系中的标准方程为($x-\sqrt{3}$)2+(y+1)2=4.
(2)∵点A的极坐标为($\sqrt{3}$,2π),
∴点A的直角坐标为($\sqrt{3}$cos2π,$\sqrt{3}sin$2π),即($\sqrt{3}$,0),
圆心C($\sqrt{3}$,-1)是线段AB的中点,点B的直角坐标为($\sqrt{3}$,-2),
∵圆C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}+2cosθ}\\{y=-1+2sinθ}\end{array}\right.,(θ为参数)$,P为圆C上任意一点,
∴设点P($\sqrt{3}+2cosθ$,-1+2sinθ),
则|PA|+|PB|=$\sqrt{(2cosθ)^{2}+(2sinθ-1)^{2}}$+$\sqrt{(2cosθ)^{2}+(2sinθ+1)^{2}}$
=$\sqrt{5+4sinθ}$+$\sqrt{5-4sinθ}$
=$\sqrt{(\sqrt{5+4sinθ}+\sqrt{5-4sinθ})^{2}}$
=$\sqrt{10+2\sqrt{25-16si{n}^{2}θ}}$,
当sinθ=0时,(|PA|+|PB|)max=$\sqrt{10+10}$=2$\sqrt{5}$,
∴|PA|+|PB|的最大值为2$\sqrt{5}$.
点评 本题考查圆在直角坐标系中标准方程的求法,考查两线段和的求法,考查两点间距离公式的应用,是中档题,解题时要认真审题,注意参数方程、直角坐标方程、极坐标方程互化公式的合理运用.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 10元 | B. | 15元 | C. | 20元 | D. | 25元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a•3=b•3,则a=b类比推出 若a•0=b•0,则a=b | |
| B. | 若(a+b)c=ac+bc类比推出 $\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$(c≠0) | |
| C. | 若(a+b)c=ac+bc类比推出 (a•b)c=ac•bc | |
| D. | 若(ab)n=anbn类比推出 (a+b)n=an+bn |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-|x-1| | B. | y=x2-2x+3 | C. | y=ln(x+1) | D. | y=2${\;}^{-\frac{x}{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
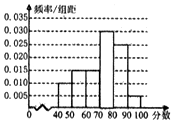 某中学选取20名优秀同学参加2015年英语应用知识竞赛,将他们的成绩(百分制)(均为整数)分成6组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.
某中学选取20名优秀同学参加2015年英语应用知识竞赛,将他们的成绩(百分制)(均为整数)分成6组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com