考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件得a
n+1+1=2(a
n+1),且a
1+1=2,所以{a
n+1}是以2为首项,2为公比的等比数列,由此能求出
an=2n-1,n∈N
*.
(Ⅱ)由已知条件得
4b1+b2+…+bn-n=
2nbn,从而得到2[(b
1+b
2+…+b
n)-n]=nb
n,进而得2(b
n+1-1)=(n+1)b
n+1-nb
n,由此得到b
n+2+b
n=2b
n+1,从而证明数列{b
n}为等差数列.
(Ⅲ)由
==-<,能证明
++…+<,n∈N*.
解答:
(本小题满分12分)
(Ⅰ)证明:因为
an+1=2an+1,n∈N*,
所以a
n+1+1=2(a
n+1),且a
1+1=2,
所以{a
n+1}是以2为首项,2为公比的等比数列.…(2分)
∴
an+1=2n,
∴
an=2n-1,n∈N
*.…(3分)
(Ⅱ)证明:因为
4b1-14b2-1•…•4bn-1=(an+1)bn,
所以
4b1+b2+…+bn-n=
2nbn,…(4分)
所以2[(b
1+b
2+…+b
n)-n]=nb
n①
2[(b
1+b
2+…+b
n+b
n+1)-(n+1)]=(n+1)b
n+1②…(6分)
②-①,得2(b
n+1-1)=(n+1)b
n+1-nb
n即(n-1)b
n+1-nb
n+2=0③
nb
n+2-(n+1)b
n+1+2=0④…(8分)
④-③,得nb
n+2-2nb
n+1+nb
n=0,
即 b
n+2+b
n=2b
n+1得b
n+2-b
n+1=b
n+1-b
n,n∈N
*…(10分)
所以数列{b
n}为等差数列.
(Ⅲ)证明因为
==-<,k=1,2,…,n.…(11分)
所以
++…+<,n∈N*.…(12分)
点评:本题考查等比数列和等差数列的证明,考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意放缩法的合理运用.



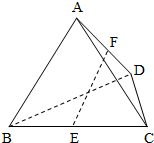 在正四面体A-BCD中,E、F分别是BC、AD的中点.
在正四面体A-BCD中,E、F分别是BC、AD的中点.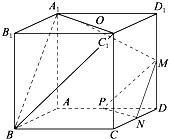 如图,在正方体ABCD-A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.