
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
在平面直角坐标系中,定义d(A,B)=|x1-x2|+|y1-y2|为两点A(x1,y1),B(x2,y2)间的“折线距离”,在此定义下,给出下列命题:
①到原点的“折线距离”为1的点的集合是一个正方形;
②到原点的“折线距离”为1的点的集合是一个圆;
③到M(-1,0),N(1,0)两点的“折线距离”相等的点的轨迹方程是x=0.
其中,正确的命题有( )
A.3个 B.2个
C.1个 D.0个
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C: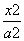 +
+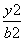 =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|AF|=6,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|AF|=6,cos∠ABF=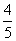 ,则C的离心率e=________.
,则C的离心率e=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
直线l:y=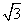 (x-2)和双曲线C:
(x-2)和双曲线C: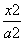 -
-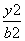 =1(a>0,b>0)交于A,B两点,且|AB|=
=1(a>0,b>0)交于A,B两点,且|AB|=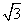 ,又l关于直线l1:y=
,又l关于直线l1:y= x对称的直线l2与x轴平行.
x对称的直线l2与x轴平行.
(1)求双曲线C的离心率;
(2)求双曲线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线C1:y=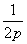 x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: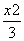 -y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )
-y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )
A.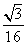 B.
B.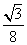
C.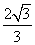 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知F1,F2分别为椭圆C: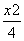 +
+ =1的左、右焦点,点P为椭圆C上的动点,则△PF1F2的重心G的轨迹方程为( )
=1的左、右焦点,点P为椭圆C上的动点,则△PF1F2的重心G的轨迹方程为( )
A.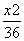 +
+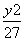 =1(y≠0) B.
=1(y≠0) B.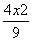 +y2=1(y≠0)
+y2=1(y≠0)
C.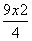 +3y2=1(y≠0) D.x2+
+3y2=1(y≠0) D.x2+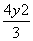 =1(y≠0)
=1(y≠0)
查看答案和解析>>
科目:高中数学 来源: 题型:
与抛物线y2=8x相切、倾斜角为135°的直线l与x轴和y轴的交点分别是A,B,那么过A,B两点的最小圆截抛物线y2=8x的准线所得的弦长为( )
A.4 B.2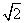
C.2 D.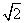
查看答案和解析>>
科目:高中数学 来源: 题型:
一个总体中的80个个体编号为0,1,2,…,79,并依次将其分为8个组,组号为0,1,…,7,要用(错位)系统抽样的方法抽取一个容量为8的样本,即规定先在第0组随机抽取一个号码,记为i,依次错位地
得到后面各组的号码,即第k组中抽取个位数字为i+k(当i+k<10)或i+k-10(当i+k≥10)的号码.在i=6时,所抽到的8个号码是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com