练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    一个总体中的80个个体编号为0,1,2，…，79，并依次将其分为8个组，组号为0,1，…，7，要用(错位)系统抽样的方法抽取一个容量为8的样本，即规定先在第0组随机抽取一个号码，记为i，依次错位地

    得到后面各组的号码，即第k组中抽取个位数字为i＋k(当i＋k<10)或i＋k－10(当i＋k≥10)的号码．在i＝6时，所抽到的8个号码是________．

     


    6,17,28,39,40,51,62,73

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若点P到直线y＝－1的距离比它到点(0,3)的距离小2，则点P的轨迹方程是________．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABP的三个顶点都在抛物线C：x2＝4y上，F为抛物线C的焦点，点M为AB的中点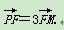

    (1)若|PF|＝3，求点M的坐标；

    (2)求△ABP面积的最大值．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对一个容量为N的总体抽取容量为n的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为p1，p2，p3，则(　　)

    A．p1＝p2<p3                             B．p2＝p3<p1

    C．p1＝p3<p2                             D．p1＝p2＝p3

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某地有居民100 000户，其中普通家庭99 000户，高收入家庭1 000户．从普通家庭中以简单随机抽样方式抽取990户，从高收入家庭中以简单随机抽样方式抽取100户进行调查，发现共有120户家庭拥有3套或3套以上住房，其中普通家庭50户，高收入家庭70户．依据这些数据并结合所掌握的统计知识，你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是________．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分(十分制)如图所示，假设得分值的中位数为me，众数为mo，平均值为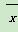，则(　　)

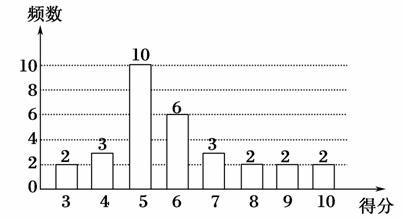
    A．me＝mo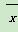＝                           B．me＝mo<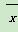

    C．me<mo<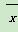                             D．mo<me<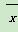

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为了增强学生的环保意识，某中学随机抽取了50名学生举行了一次环保知识竞赛，并将本次竞赛的成绩(得分均为整数，满分100分)整理，制成下表：

    成绩

    [40，

    50)

    [50，

    60)

    [60，

    70)

    [70，

    80)

    [80，

    90)

    [90，

    100]

    频数

    2

    3

    14

    15

    12

    4

    (1)作出被抽查学生成绩的频率分布直方图；

    (2)若从成绩在[40,50)中选一名学生，从成绩在[90,100]中选2名学生，共3名学生召开座谈会，求[40,50)组中学生A1和[90,100]组中学生B1同时被选中的概率．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某校为了比较“传统式教学法”与该校所创立的“三步式教学法”的教学效果．共选100名学生随机分成两个班，每班50名学生，其中一班采取“传统式教学法”，二班实行“三步式教学法”．

    (1)若全校共有学生2 000名，其中男生1 100名，现抽取100名学生对两种教学法的受欢迎程度进行问卷调查，应抽取多少名女生？

    (2)表1,2分别为实行“传统式教学法”与“三步式教学法”后的数学成绩：

    表1

    数学成绩

    90分以下

    90～120分

    120～140分

    140分以上

    频数

    15

    20

    10

    5

    表2

    数学成绩

    90分以下

    90～120分

    120～140分

    140分以上

    频数

    5

    40

    3

    2

    完成下面2×2列联表，并回答能否在犯错误的概率不超过0.01的前提下认为这两种教学法有差异．

     

     

    120分以下(人数)

    120分以上(人数)

    总计(人数)

    一班

    二班

    总计

    参考公式：K2＝其中n＝a＋b＋c＋d.

    参考数据：

    P(K2≥k0)

    0.40

    0.25

    0.10

    0.05

    0.010

    0.005

    k0

    0.708

    1.323

    2.706

    3.841

    6.635

    7.879

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    (x2－x＋1)10展开式中x3项的系数为(　　)

    A．－210                                B．210

    C．30                                   D．－30

    查看答案和解析>>

    同步练习册答案