练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     已知函数f(x)＝cos(2x－)＋sin2x－cos2x.

    (1)求函数f(x)的最小正周期及图象的对称轴方程；

    (2)设函数g(x)＝[f(x)]2＋f(x)，求g(x)的值域．


    解：(1)f(x)＝cos2x＋sin2x－cos2x

    ＝sin2x－cos2x＝sin(2x－)．

    ∴最小正周期T＝＝π.

    由2x－＝kπ＋，k∈Z，得x＝＋，k∈Z.

    ∴函数图象的对称轴方程为x＝＋，k∈Z.

    (2)g(x)＝[f(x)]2＋f(x)

    ＝sin2(2x－)＋sin(2x－)

    ＝[sin(2x－)＋]2－.

    当sin(2x－)＝－时，g(x)取得最小值－，

    当sin(2x－)＝1时，g(x)取得最大值2.

    ∴g(x)的值域为[－，2]．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数，（为常数），函数图象上横坐标为的点处的切线，与函数的图象相切．

    （Ⅰ）求直线的方程及的值；

    （Ⅱ）若，求函数的极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数（）的图象经过两点，则的最小值为____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


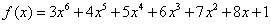     用秦九韶算法计算多  

    项式当x=0.4时的值时,需要做乘法和加法的次数分别是 (    )

    A. 6 , 6           B. 5 , 6     C. 5 , 5       D. 6 , 5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     给出下列五个命题：

    ①函数的图像关于点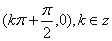对称；

    ②函数是最小正周期为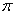的周期函数；

    ③设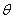为第二象限的角，则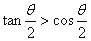，且；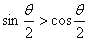

    ④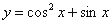的最小值为-1；

    其中正确的命题是                。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有如下四个结论：

    ①分别在两个平面内的两条直线一定是异面直线；

    ②过平面的一条斜线有一个平面与平面垂直；

    ③ “”是“”的必要条件；

    ④命题“”的否定是“”．

    其中正确结论的个数为（   ）

    A．4          B．3          C．2          D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     “”，“”，若是的充分不必要条件，则的取值范围是             ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知，如果是的充分不必要条件，则实数的取值范围是(   )   

    A.      B.      C.      D.

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年江西省高三上学期第三次月考文科数学试卷（解析版） 题型：填空题

    已知直线与函数的图象恰有三个不同的公共点，则实数的取值范围是 ．

    查看答案和解析>>

    同步练习册答案