
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 本题即找出哪个函数是偶函数,在所给的4个选项中,只有②③中的函数是偶函数,其余的都不是偶函数,从而得出结论.
解答 解:由题意可得,图象关于y轴对称的函数为偶函数.
对于①y=$\sqrt{x}$,定义域为[0,+∞),不关于原点对称,不具奇偶性;
对于②y=x2,则为幂函数,显然为偶函数;
对于③y=2|x|,定义域为R,f(-x)=2|-x|=2|x|=f(x),则为偶函数;
对于④y=|lnx|,定义域为(0,+∞),不关于原点对称,不具奇偶性.
故只有②③中的函数是偶函数,其余的都不是偶函数,
故选C.
点评 本题主要考查偶函数的定义和性质,判断函数的奇偶性,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
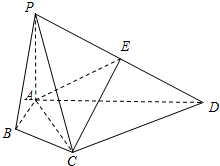 在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.
在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x∈R|-2≤x≤2} | B. | {x∈R|-1≤x≤2} | C. | {x∈R|1≤x≤2} | D. | {x∈R|-1≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com