Question

7．（Ⅰ）已知α角的终边经过点（t-2，t ²-1）且cosα≤0，sinα＞0，求实数t的取值范围；
（Ⅱ）试作出函数 $f（x）=\frac{sinx}{{|{sinx}|}}$在（-2π，2π）上的图象．

Answer 1

分析 （Ⅰ）直接根据α的终边在第二象限或y轴正向上，得到关于t的不等式组，解得即可，
（Ⅱ）先化为分段函数，再画图即可．

解答 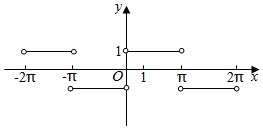解：（Ⅰ）依题意，α的终边在第二象限或y轴正向上，∴$\left\{\begin{array}{l}t-2≤0\\{t^2}-1＞0\end{array}\right.$$⇒\left\{\begin{array}{l}t≤2\\ t?-1或ora＞1\end{array}\right.$，
∴t＜-1或1＜t≤2．
（Ⅱ）$f（x）=\frac{sinx}{{|{sinx}|}}$=$\left\{\begin{array}{l}-1，x∈（-π，0）∪（π，2π）\\ 1，x∈（-2π，-π）∪（0，π）\end{array}\right.$
作出图象如图．

点评 本题考查了任意角的三角函数的定义以及函数图象的画法，属于基础题．